��Ŀ����
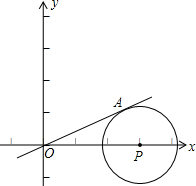 ����֪������һ�κ���y=k1x+b1��y=k2x+b2����k1=k2ʱ��������һ�κ�����ͼ���ƽ�У���ô����һ�κ�����ͼ��ʲô��������ֱ�أ��������Ǿ���̽����
����֪������һ�κ���y=k1x+b1��y=k2x+b2����k1=k2ʱ��������һ�κ�����ͼ���ƽ�У���ô����һ�κ�����ͼ��ʲô��������ֱ�أ��������Ǿ���̽������1����һ��
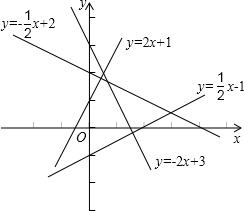
��ͬһƽ��ֱ������ϵ�»���һ�κ���y=2x+1��y=-2x+3��y=
| 1 |
| 2 |
| 1 |
| 2 |
��2����һ��
��ϸ�۲�ͼ����ĸ�һ�κ����Ľ���ʽ������룺��
k1•k2=-1
k1•k2=-1
ʱ������һ�κ���y=k1x+b1��y=k2x+b2��ͼ�����ֱ����3����һ��
���ã�2���еĽ��۽������������ͼ����֪����������y=
| 1 |
| 2 |
��������1���ֱ����ֱ����������Ľ��㣬Ȼ���������ȷ��һ��ֱ�ߣ��������㷨����ֱ��ͼ�ɣ�
��2�����ͼ����ݻ��ഹֱ����ֱ�߽���ʽ��kֵ���
��3�����ݣ�2���Ľ������ֱ��AP��kֵ��Ȼ�����ֱ��AP�Ľ���ʽ����OA�Ľ���ʽ�������õ���A�����꣬�����ù��ɶ������OA�ij��ȣ��ٴ����ù��ɶ������PA�ij��ȣ�Ȼ�����Բ�������ʽ��ʽ���㼴�ɵý⣮
��2�����ͼ����ݻ��ഹֱ����ֱ�߽���ʽ��kֵ���
��3�����ݣ�2���Ľ������ֱ��AP��kֵ��Ȼ�����ֱ��AP�Ľ���ʽ����OA�Ľ���ʽ�������õ���A�����꣬�����ù��ɶ������OA�ij��ȣ��ٴ����ù��ɶ������PA�ij��ȣ�Ȼ�����Բ�������ʽ��ʽ���㼴�ɵý⣮
��� �⣺��1����x=0ʱ��y=1��y=0ʱ��2x+1=0�����x=-
�⣺��1����x=0ʱ��y=1��y=0ʱ��2x+1=0�����x=-
��
���ԣ�ֱ��y=2x+1�����㣨0��1����-
��0����
�ڵ�x=0ʱ��y=3����y=0ʱ��-2x+3=0�����x=
��
���ԣ�ֱ��y=-2x+3�����㣨0��3����
��0����
�۵�x=0ʱ��y=-1����y=0ʱ��
x-1=0�����x=2��
���ԣ�ֱ��y=
x-1�����㣨0��-1����2��0����
�ܵ�x=0ʱ��y=2����y=0ʱ��-
x+2=0�����x=4��
���ԣ�ֱ��y=-
x+2�����㣨0��2����4��0����
��ͼ��ͼ��ʾ��
��2����ͼ��֪��y=2x+1��y=-
x+2��ֱ��y=-2x+3��y=
x-1��ֱ��
��2����-
��=-1��-2��
=-1��
����뵱k1•k2=-1ʱ��y=k1x+b1��y=k2x+b2��ͼ�����ֱ��
�ʴ�Ϊ��k1•k2=-1��
��3�����ݣ�2���Ľ��ۣ�
������������y=
x��ͼ��͡�P�����ڵ�A��
��ֱ��AP��kֵ����-2��
���ԣ���ֱ��AP�Ľ���ʽΪy=-2x+b��
��OP=3��
���P��������3��0����
��-2��3+b=0��
���b=6��
��ֱ��AP�Ľ���ʽΪy=-2x+6��
����
��
���
��
���ԣ�OA=
=
��
AP=
=
=
��
��P�����=��•AP2=��•��
��2=
�У�
 �⣺��1����x=0ʱ��y=1��y=0ʱ��2x+1=0�����x=-
�⣺��1����x=0ʱ��y=1��y=0ʱ��2x+1=0�����x=-| 1 |
| 2 |
���ԣ�ֱ��y=2x+1�����㣨0��1����-
| 1 |
| 2 |
�ڵ�x=0ʱ��y=3����y=0ʱ��-2x+3=0�����x=
| 3 |
| 2 |
���ԣ�ֱ��y=-2x+3�����㣨0��3����
| 3 |
| 2 |
�۵�x=0ʱ��y=-1����y=0ʱ��
| 1 |
| 2 |
���ԣ�ֱ��y=
| 1 |
| 2 |
�ܵ�x=0ʱ��y=2����y=0ʱ��-
| 1 |
| 2 |
���ԣ�ֱ��y=-
| 1 |
| 2 |
��ͼ��ͼ��ʾ��
��2����ͼ��֪��y=2x+1��y=-
| 1 |
| 2 |
| 1 |
| 2 |
��2����-
| 1 |
| 2 |
| 1 |
| 2 |
����뵱k1•k2=-1ʱ��y=k1x+b1��y=k2x+b2��ͼ�����ֱ��
�ʴ�Ϊ��k1•k2=-1��
��3�����ݣ�2���Ľ��ۣ�
������������y=
| 1 |
| 2 |
��ֱ��AP��kֵ����-2��
���ԣ���ֱ��AP�Ľ���ʽΪy=-2x+b��
��OP=3��
���P��������3��0����
��-2��3+b=0��
���b=6��
��ֱ��AP�Ľ���ʽΪy=-2x+6��
����
|
���
|
���ԣ�OA=
(
|
| 6 |
| 5 |
| 5 |
AP=
| OP2-OA2 |
9-
|
| 3 |
| 5 |
| 5 |
��P�����=��•AP2=��•��
| 3 |
| 5 |
| 5 |
| 9 |
| 5 |
�����������Ƕ�һ�κ������ۺϿ��飬��Ҫ�漰�������㷨��һ�κ���ͼ��������ֱ�߽���ʽ��ֱ�ߵĽ��㣬���ɶ�����Ӧ�ã����ۺ��⣬���ѶȲ�������Ŀ��Ϣ��ȷ����ͼ���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2013•��ͨ�����տư�ˣ��£��̲�һ��ϰ���̽���о�������֪����һ�κ���y=x-1��ͼ�����������������y=x��ͼ������ƽ��1����λ���ȵõ����Ƶģ�����
��2013•��ͨ�����տư�ˣ��£��̲�һ��ϰ���̽���о�������֪����һ�κ���y=x-1��ͼ�����������������y=x��ͼ������ƽ��1����λ���ȵõ����Ƶģ����� ����֪������һ�κ���y=k1x+b1��y=k2x+b2����k1=k2ʱ��������һ�κ�����ͼ���ƽ�У���ô����һ�κ�����ͼ��ʲô��������ֱ�أ��������Ǿ���̽����
����֪������һ�κ���y=k1x+b1��y=k2x+b2����k1=k2ʱ��������һ�κ�����ͼ���ƽ�У���ô����һ�κ�����ͼ��ʲô��������ֱ�أ��������Ǿ���̽���� x-1��y=-
x-1��y=- x-1��y=-
x-1��y=- x+2��ͼ��
x+2��ͼ�� x��ͼ��͡�P�����ڵ�A����P��x���ϣ�OP=3���ף����P�������
x��ͼ��͡�P�����ڵ�A����P��x���ϣ�OP=3���ף����P�������