摘要： 如图:⊙O1与⊙O2外切于点P.O1O2的延长线交⊙O2于点A.AB切⊙O1于点B.交⊙O2于点C.BE是⊙O1的直径.过点B作BF┴O1P.垂足为F.延长BF交PE于点G. (1)求证:PB2=PG·PE, (2)若PF= .tan∠A= .求:O1O2的长.
网址：http://m.1010jiajiao.com/timu3_id_438065[举报]
已知：如图，⊙O1与⊙O2外切于点O，以直线O1O2为x轴，O为坐标原点，建立平面直角坐标系．在x轴上方的两圆的外公切线AB与⊙O1相切于点A，与⊙O2相切于点B，直线AB交y轴于点c，若OA=3
，OB=3．
（1）求经过O1、C、O2三点的抛物线的解析式；
（2）设直线y=kx+m与（1）中的抛物线交于M、N两点，若线段MN被y轴平分，求k的值；
（3）在（2）的条件下，点D在y轴负半轴上．当点D的坐标为何值时，四边形M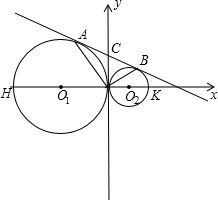
DNC是矩形？
查看习题详情和答案>>
| 3 |
（1）求经过O1、C、O2三点的抛物线的解析式；
（2）设直线y=kx+m与（1）中的抛物线交于M、N两点，若线段MN被y轴平分，求k的值；
（3）在（2）的条件下，点D在y轴负半轴上．当点D的坐标为何值时，四边形M
DNC是矩形？
查看习题详情和答案>>
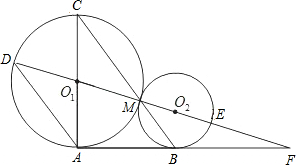已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
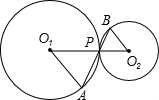如图，⊙O1与⊙O2外切于点P，过点P的直线AB分别交⊙O1，⊙O2于点A，B．已知O1A：O2B=3：2，则PA：PB=
37、如图，⊙O1与⊙O2外切于点C，一条外公切线切两圆于点A，B，已知⊙O1的半径是9，⊙O2的半径是3，求∠BAC的度数．
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=