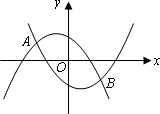
摘要：解:(1)设的解析式为y＝. ∵与x轴的交点A.顶点坐标是. 并且与关于x轴对称. ∴经过点A.顶点坐标是(0.4). -- 1分 ∴y＝. ------------- 2分 ∴0＝4a+4 得a＝-1. ∴的解析式为.- --------- 3分 (2)设B() ∵点B在上. ∴B() ----------- 4分 ∵四边形ABCD是平行四边形.A.C关于O对称. ∴B.D关于原点O对称. ∴D(). -------------- 6分 将D()的坐标代入: 可知 左边＝右边. ∴点D在上. --------------- 7分 (3)设□ABCD的面积为S.则S＝2×. (I)当点B在x轴上方时.＞0. ∴.它是关于的正比例函数且S随的增大而增大. ∴S既无最大值也无最小值.--------------- 8分 (II)当点B在x轴下方时.-4≤＜0. ∴.它是关于的正比例函数且S随的增大而减小. ∴当＝-4时.S有最大值16.但它没有最小值. 此时B在y轴上.它的对称点D也在y轴上.------- 9分 ∴AC⊥BD. ∴□ABCD是菱形.--------------10分 此时. --------------11分
网址：http://m.1010jiajiao.com/timu3_id_437481[举报]
已知二次函数y＝x2＋ax＋a－2．
(1)求证：不论a为何实数，此函数图象与x轴总有两个交点．
(2)设a＜0，当此函数图象与x轴的两个交点的距离为
时，求出此二次函数的解析式．
(3)若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为
，若存在求出P点坐标，若不存在请说明理由．
已知：抛物线C1：y＝ax2＋4ax＋4a－5的顶点为P，与x轴相交于A、B两点(点A在点B的左边)，点B的横坐标是1．
(1)
求抛物线的解析式和顶点P的坐标；(2)将抛物线沿
x轴翻折，再向右平移，平移后的抛物线C2的顶点为M，当点P、M关于点B成中心对称时，求平移后的抛物线C2的解析式；(3)直线y＝－
x＋m与抛物线C1、C2的对称轴分别交于点E、F，设由点E、P、F、M构成的四边形的面积为s，试用含m的代数式表示s．
已知：抛物线y＝ax2－4ax＋m与x轴的一个交点为A(1，0)．
(1)求抛物线与x轴的另一个交点B的坐标；
(2)点C是抛物线与y轴的交点，且△ABC的面积为3，求此抛物线的解析式；
(3)点D是(2)中开口向下的抛物线的顶点．抛物线上点C的对称点为Q，把点D沿对称轴向下平移5个单位长度，设这个点为P；点M、N分别是x轴、y轴上的两个动点，当四边形PQMN的周长最短时，求PN＋MN＋QM的长．(结果保留根号)
与直线y＝－x＋2只有一个公共点P，则称P为切点．
与直线y＝kx＋6只有一个公共点M，求：当k＜0时两个函数的解析式和切点M的坐标；
时，设y1＝－ax2－ax＋1与x轴分别交于M，N两点(M在N的左边)，y2＝ax2－ax－1与x轴分别交于E，F两点(E在F的左边)，观察M，N，E，F四点坐标，请写出一个你所得到的正确结论，并说明理由；