题目内容
已知:抛物线y=ax2-4ax+m与x轴的一个交点为A(1,0).
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点C是抛物线与y轴的交点,且△ABC的面积为3,求此抛物线的解析式;
(3)点D是(2)中开口向下的抛物线的顶点.抛物线上点C的对称点为Q,把点D沿对称轴向下平移5个单位长度,设这个点为P;点M、N分别是x轴、y轴上的两个动点,当四边形PQMN的周长最短时,求PN+MN+QM的长.(结果保留根号)
答案:
解析:
解析:
|
解:(1)依题意,抛物线的对称轴为 ∴由抛物线的对称性,可得抛物线与x轴的另一个交点B的坐标为(3,0) 1分 (2)
∴C(0,3a). 2分 AB=2,OC= S△ABC= ∴ ∴ ∴所求抛物线的解析式为 (3)依题意知,抛物线的解析式为: ∴点D(2,1),C(0,-3),P(2,-4). 设Q(x,y), ∴点Q坐标( 分别作P、Q关于x轴、y轴的对称点 ∴ 过 ∴ 由作图可知,PN= ∴PN+MN+QM= ∴PN+MN+QM的长为 |

练习册系列答案
相关题目


 的两个实数根,与
的两个实数根,与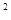 +bx+c与
+bx+c与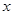 轴交于
轴交于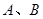 两点,若
两点,若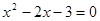 的两个实数根,与
的两个实数根,与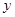 轴交于点
轴交于点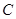 (0,3),
(0,3),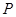 ,使
,使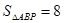 .
. +bx+c与
+bx+c与 轴交于
轴交于 两点,若
两点,若 的两个实数根,与
的两个实数根,与 轴交于点
轴交于点 (0,3),
(0,3),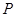 ,使
,使 .
.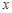 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒). (3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.