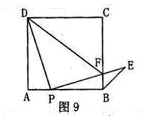
摘要:25. 如图9.点P是正方形ABCD边AB上一点.连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE. PE交边BC于点F.连接BE.DF. (1)求证:∠ADP=∠EPB, (2)求∠CBE的度数, (3)当的值等于多少时.△PFD∽△BFP?并说明理由.
网址:http://m.1010jiajiao.com/timu3_id_435898[举报]
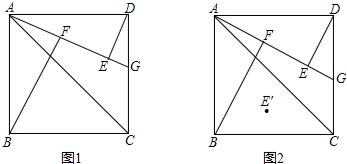
如图1,点G是正方形ABCD的边DC上任意一点(不与D、C两点重合),连接AC、AG,作BF⊥AG于点F,DE⊥AG于点E.
(1)试判断线段DE、BF的长的大小关系,说明理由;
(2)试探究线段EF与DE、BF的长有何等量关系,并给予证明;
(3)如本题图2,若E′是点E关于直线AC的对称点,连接BE′,试探究DG、AG满足什么条件时,射线BE′是∠FBC的角平分线?为什么?
查看习题详情和答案>>
(1)试判断线段DE、BF的长的大小关系,说明理由;
(2)试探究线段EF与DE、BF的长有何等量关系,并给予证明;
(3)如本题图2,若E′是点E关于直线AC的对称点,连接BE′,试探究DG、AG满足什么条件时,射线BE′是∠FBC的角平分线?为什么?

27、已知如图1,点P是正方形ABCD的BC边上一动点,AP交对角线BD于点E,过点B作BQ⊥AP于G点,交对角线AC于F,交边CD于Q点.
(1)小聪在研究图形时发现图中除等腰直角三角形外,还有几对三角形全等.请你写出其中三对全等三角形,并选择其中一对全等三角形证明;
(2)小明在研究过程中连接PE,提出猜想:在点P运动过程中,是否存在∠APB=∠CPF?若存在,点P应满足何条件并说明理由;若不存在,为什么?

查看习题详情和答案>>
(1)小聪在研究图形时发现图中除等腰直角三角形外,还有几对三角形全等.请你写出其中三对全等三角形,并选择其中一对全等三角形证明;
(2)小明在研究过程中连接PE,提出猜想:在点P运动过程中,是否存在∠APB=∠CPF?若存在,点P应满足何条件并说明理由;若不存在,为什么?

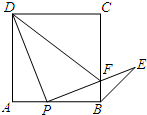 如图,动点P是正方形ABCD边AB上运动(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.
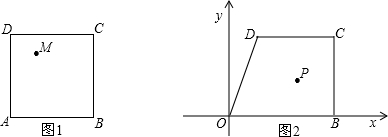
如图,动点P是正方形ABCD边AB上运动(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.(1)求证:∠ADP=∠EPB.
(2)若正方形ABCD边长为4,点F能否为边BC的中点?如果能,请你求出AP的长;如果不能,请说明理由.
(3)当
| AP | AB |
 (2)求∠CBE的度数;
(2)求∠CBE的度数;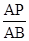 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.