题目内容
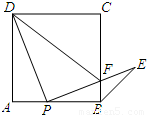
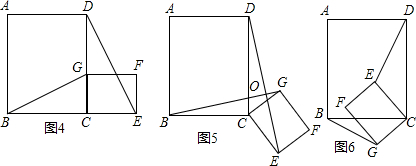
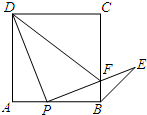 如图,动点P是正方形ABCD边AB上运动(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.
如图,动点P是正方形ABCD边AB上运动(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.(1)求证:∠ADP=∠EPB.
(2)若正方形ABCD边长为4,点F能否为边BC的中点?如果能,请你求出AP的长;如果不能,请说明理由.
(3)当
| AP | AB |
分析:(1)根据∠ADP与∠EPB都是∠APD的余角,根据同角的余角相等,即可求证;
(2)假设F为BC的中点,且正方形边长为4,求出FB=2,再由(1)得出的∠ADP=∠EPB,加上一对直角相等,利用两对对应角相等的两三角形相似可得出△PAD和△PFB相似,由相似得比例,将各自的值代入得出关于AP的方程,求出根的判别式小于0,得到此方程无解,故F不能为BC的中点;
(3)这两个三角形是直角三角形,若相似,则对应边的比相等,即可求得
的值.
(2)假设F为BC的中点,且正方形边长为4,求出FB=2,再由(1)得出的∠ADP=∠EPB,加上一对直角相等,利用两对对应角相等的两三角形相似可得出△PAD和△PFB相似,由相似得比例,将各自的值代入得出关于AP的方程,求出根的判别式小于0,得到此方程无解,故F不能为BC的中点;
(3)这两个三角形是直角三角形,若相似,则对应边的比相等,即可求得
| AP |
| AB |
解答:(1)证明:∵四边形ABCD是正方形.
∴∠A=∠PBC=90°,AB=AD,
∴∠ADP+∠APD=90°,
∵∠DPE=90°,
∴∠APD+∠EPB=90°,
∴∠ADP=∠EPB;
(2)解:假设F为BC的中点,可得BF=CF=
BC=2,
∵∠ADP=∠EPB,∠A=∠ABC=90°,
∴△ADP∽△BPF,
∴
=
,即
=
,
整理得:AP2-4AP+8=0,
∵b2-4ac=16-32=-16<0,
∴此方程无解,
则点F不能为边BC的中点;
(3)解:当
=
时,△PFD∽△BFP,理由为:
设AD=AB=a,则AP=PB=
a,
∴BF=BP•
=
a,
∴PD=
=
a,PF=
=
a,
∴
=
=
,
又∵∠DPF=∠PBF=90°,
∴△PFD∽△BFP.
∴∠A=∠PBC=90°,AB=AD,
∴∠ADP+∠APD=90°,
∵∠DPE=90°,
∴∠APD+∠EPB=90°,
∴∠ADP=∠EPB;
(2)解:假设F为BC的中点,可得BF=CF=
| 1 |
| 2 |
∵∠ADP=∠EPB,∠A=∠ABC=90°,
∴△ADP∽△BPF,
∴
| AD |
| BP |
| AP |
| BF |
| 4 |
| 4-AP |
| AP |
| 2 |
整理得:AP2-4AP+8=0,
∵b2-4ac=16-32=-16<0,
∴此方程无解,
则点F不能为边BC的中点;
(3)解:当
| AP |
| AB |
| 1 |
| 2 |
设AD=AB=a,则AP=PB=
| 1 |
| 2 |
∴BF=BP•
| AP |
| AD |
| 1 |
| 4 |
∴PD=
| AD2+AP2 |
| ||
| 2 |
| PB2+BF2 |
| ||
| 4 |
∴
| PB |
| PD |
| BF |
| PF |
| ||
| 5 |
又∵∠DPF=∠PBF=90°,
∴△PFD∽△BFP.
点评:本题主要考查了正方形的性质,以及三角形相似的判定与性质,是一道相似形综合题.正确探究三角形相似的性质是解题的关键.

练习册系列答案
相关题目
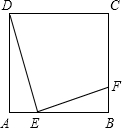 如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.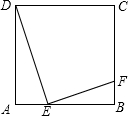 如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
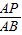 的值等于多少时,△PFD∽△BFP?并说明理由.
的值等于多少时,△PFD∽△BFP?并说明理由.