题目内容
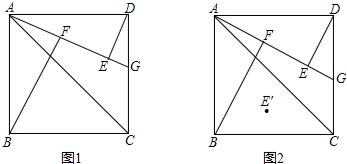
如图1,点G是正方形ABCD的边DC上任意一点(不与D、C两点重合),连接AC、AG,作BF⊥AG于点F,DE⊥AG于点E.
(1)试判断线段DE、BF的长的大小关系,说明理由;
(2)试探究线段EF与DE、BF的长有何等量关系,并给予证明;
(3)如本题图2,若E′是点E关于直线AC的对称点,连接BE′,试探究DG、AG满足什么条件时,射线BE′是∠FBC的角平分线?为什么?
(1)试判断线段DE、BF的长的大小关系,说明理由;
(2)试探究线段EF与DE、BF的长有何等量关系,并给予证明;
(3)如本题图2,若E′是点E关于直线AC的对称点,连接BE′,试探究DG、AG满足什么条件时,射线BE′是∠FBC的角平分线?为什么?

分析:(1)由正方形的性质就可以得出AB=AD,由BF⊥AG于点F,DE⊥AG据可以得出∠BAF=∠ADE,通过证明△ABF≌△DAE就可以得出结论;
(2)通过证明△ABF≌△DAE就可以得出AF=DE,BF=AE就可以得出结论BF=DE+EF;
(3)连接BE′,AE′,EE′,就可以得出AE=AE′,∠E′AC=∠EAC,就可以得出△BAE′≌△DAE,就可以得出∠ABE′=∠ADE,进而得出∠CBE′=∠CDE,可以得出∠ABF=∠FBE′=∠CBE′,就可以得出∠DAE=30°,进而得出结论AG=2DG.
(2)通过证明△ABF≌△DAE就可以得出AF=DE,BF=AE就可以得出结论BF=DE+EF;
(3)连接BE′,AE′,EE′,就可以得出AE=AE′,∠E′AC=∠EAC,就可以得出△BAE′≌△DAE,就可以得出∠ABE′=∠ADE,进而得出∠CBE′=∠CDE,可以得出∠ABF=∠FBE′=∠CBE′,就可以得出∠DAE=30°,进而得出结论AG=2DG.
解答:解:(1)DE<BF
理由:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,
AB=BC=CD=DA,∠BAC=∠DAC=45°.
∵BF⊥AG,DE⊥AG,
∴∠AED=∠GED=AFB=90°,
∴∠ADE+∠DAE=90°.,∠ABF+∠BAF=90°,
∵∠ADE+∠EDG=90°,∠BAF+∠DAE=90°
∴∠DAE=∠GDE=∠ABF.
在△ABF和△DAE中,
,
∴△ABF≌△DAE(AAS),
∴AF=DE.
∵∠BAC=45°,
∴∠BAC+∠CAF=∠BAF>45°.
∵∠BAF+∠ABF=90°,
∴∠ABF<45°,
∴∠ABF<∠BAF,
∴AF<BF,
∴DE∠BF;
(2)BF=DE+EF
理由:∵△ABF≌△DAE(AAS),
∴BF=AE,AF=DE.∠ABF=∠DAE.
∵AE=AF+EF,
∴BF=DE+EF;
(3)AG=2DG
连接BE′,AE′,EE′
∵E′是点E关于直线AC对称,
∴AE=AE′,∠E′AC=∠EAC.
∵∠BAC=∠DAC,
∴∠BAC-,∠E′AC=∠DAC-∠EAC,
即∠ABE′=∠DAE.
在△BAE′和△DAE中,
,
∴△BAE′≌△DAE(SAS),
∴∠ABE′=∠ADE,
∴∠CBE′=∠CDE,
∴∠CBE′=∠ABF.
∵BE′是∠FBC的角平分线,
∴∠ABF=∠FBE′=∠CBE′.
∵∠ABF+∠FBE′+∠CBE′=90°,
∴∠ABF=30°,
∴∠DAE=30°,
∴在△RtADG中,
AG=2DG.
理由:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,
AB=BC=CD=DA,∠BAC=∠DAC=45°.
∵BF⊥AG,DE⊥AG,
∴∠AED=∠GED=AFB=90°,
∴∠ADE+∠DAE=90°.,∠ABF+∠BAF=90°,
∵∠ADE+∠EDG=90°,∠BAF+∠DAE=90°
∴∠DAE=∠GDE=∠ABF.
在△ABF和△DAE中,
|
∴△ABF≌△DAE(AAS),
∴AF=DE.
∵∠BAC=45°,
∴∠BAC+∠CAF=∠BAF>45°.
∵∠BAF+∠ABF=90°,
∴∠ABF<45°,
∴∠ABF<∠BAF,
∴AF<BF,
∴DE∠BF;
(2)BF=DE+EF
理由:∵△ABF≌△DAE(AAS),
∴BF=AE,AF=DE.∠ABF=∠DAE.
∵AE=AF+EF,
∴BF=DE+EF;
(3)AG=2DG
连接BE′,AE′,EE′
∵E′是点E关于直线AC对称,
∴AE=AE′,∠E′AC=∠EAC.

∵∠BAC=∠DAC,
∴∠BAC-,∠E′AC=∠DAC-∠EAC,
即∠ABE′=∠DAE.
在△BAE′和△DAE中,
|
∴△BAE′≌△DAE(SAS),
∴∠ABE′=∠ADE,
∴∠CBE′=∠CDE,
∴∠CBE′=∠ABF.
∵BE′是∠FBC的角平分线,
∴∠ABF=∠FBE′=∠CBE′.
∵∠ABF+∠FBE′+∠CBE′=90°,
∴∠ABF=30°,
∴∠DAE=30°,
∴在△RtADG中,
AG=2DG.
点评:本题考查了正方形的性质的运用,三角形边角关系的运用,大角对大边,直角三角形的性质的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,轴对称的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目

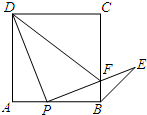 如图,动点P是正方形ABCD边AB上运动(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.
如图,动点P是正方形ABCD边AB上运动(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.
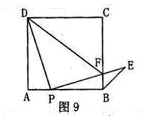 (2)求∠CBE的度数;
(2)求∠CBE的度数;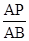 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.