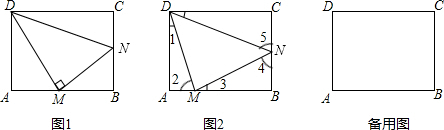
摘要:如图.矩形ABCD中.AB=6.BC=2.点O是AB的中点.点P在AB的延长线上.且BP=3.一动点E从O点出发.以每秒1个单位长度的速度沿OA匀速运动.到达A点后.立即以原速度沿AO返回,另一动点F从P点发发.以每秒1个单位长度的速度沿射线PA匀速运动.点E.F同时出发.当两点相遇时停止运动.在点E.F的运动过程中.以EF为边作等边△EFG.使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒. (1)当等边△EFG的边FG恰好经过点C时.求运动时间t的值, (2)在整个运动过程中.设等边△EFG和矩形ABCD重叠部分的面积为S.请直接写出S与t之间的函数关系式和相应的自变量t的取值范围, (3)设EG与矩形ABCD的对角线AC的交点为H.是否存在这样的t.使△AOH是等腰三角形?若存大.求出对应的t的值,若不存在.请说明理由. 考点:相似三角形的判定与性质,根据实际问题列二次函数关系式,等腰三角形的性质,等边三角形的性质,矩形的性质,解直角三角形. 专题:代数几何综合题,动点型,分类讨论. 分析:(1)当边FG恰好经过点C时.∠CFB=60°.BF=3﹣t.在Rt△CBF中.解直角三角形可求t的值, (2)按照等边△EFG和矩形ABCD重叠部分的图形特点.分为0≤t<1.1≤t<3.3≤t<4.4≤t<6四种情况.分别写出函数关系式, (3)存在.当△AOH是等腰三角形时.分为AH=AO=3.HA=HO.OH=OA三种情况.分别画出图形.根据特殊三角形的性质.列方程求t的值. 解答:解:(1)当边FG恰好经过点C时.∠CFB=60°.BF=3﹣t.在Rt△CBF中.BC=2.tan∠CFB=.即tan60=.解得BF=2.即3﹣t=2.t=1.∴当边FG恰好经过点C时.t=1, (2)当0≤t<1时.S=2t+4, 当1≤t<3时.S=﹣t2+3t+, 当3≤t<4时.S=﹣4t+20, 当4≤t<6时.S=t2﹣12t+36, (3)存在. 理由如下:在Rt△ABC中.tan∠CAB==. ∴∠CAB=30°.又∵∠HEO=60°.∴∠HAE=∠AHE=30°. ∴AE=HE=3﹣t或t﹣3. 1)当AH=AO=3时..过点E作EM⊥AH于M.则AM=AH=. 在Rt△AME中.cos∠MAE═.即cos30°=. ∴AE=.即3﹣t=或t﹣3=. ∴t=3﹣或t=3+. 2)当HA=HO时.则∠HOA=∠HAO=30°. 又∵∠HEO=60°.∴∠EHO=90°.EO=2HE=2AE. 又∵AE+EO=3.∴AE+2AE=3.AE=1. 即3﹣t=1或t﹣3=1.∴t=2或t=4, 3)当OH=OA时..则∠OHA=∠OAH=30°. ∴∠HOB=60°=∠HEB.∴点E和点O重合. ∴AE=3.即3﹣t=3或t﹣3=3.t=6或t=0, 综上所述.存在5个这样的t值.使△AOH是等腰三角形.即t=3﹣或t=3+或t=2或t=2或t=0. 点评:本题考查了特殊三角形.矩形的性质.相似三角形的判定与性质.解直角三角形的有关知识.关键是根据特殊三角形的性质.分类讨论.
网址:http://m.1010jiajiao.com/timu3_id_435749[举报]
如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由D向C运动.沿直线AP翻折△ADP,形成如下四种情形.设DP=x,△ADP和矩形重叠部分(阴影)的面积为y.
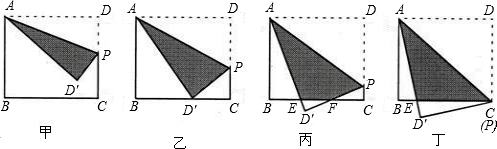
(1)如图丁,当点P运动到与C重合时,求重叠部分的面积y;
(2)如图乙,当点P运动到何处时,翻折△ADP后,点D恰好落在BC边上这时重叠部分的面积y等于多少?
(3)阅读材料:已知锐角α≠45°,tan2α是角2α的正切值,它可以用角α的正切值tanα来表示,即tan2α=
(α≠45°).根据上述阅读材料,求出用x表示y的解析式,并指出x的取值范围.
(提示:在图丙中可设∠DAP=a) 查看习题详情和答案>>

(1)如图丁,当点P运动到与C重合时,求重叠部分的面积y;
(2)如图乙,当点P运动到何处时,翻折△ADP后,点D恰好落在BC边上这时重叠部分的面积y等于多少?
(3)阅读材料:已知锐角α≠45°,tan2α是角2α的正切值,它可以用角α的正切值tanα来表示,即tan2α=
| 2tanα | 1-(tanα)2 |
(提示:在图丙中可设∠DAP=a) 查看习题详情和答案>>
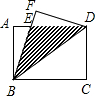 如图,矩形ABCD中,AB=3,BC=4,如果将矩形沿对角线BD折叠,那么图中阴影部分的面积是( )
如图,矩形ABCD中,AB=3,BC=4,如果将矩形沿对角线BD折叠,那么图中阴影部分的面积是( )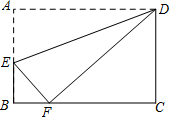 如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿DE折叠,点A恰好落在边BC上的点F处.若AE=5,BF=3,则tan∠FDC的值为( )
如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿DE折叠,点A恰好落在边BC上的点F处.若AE=5,BF=3,则tan∠FDC的值为( )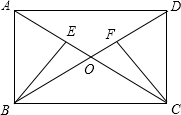 已知:如图,矩形ABCD中,对角线AC与BD交于点O,点E、F分别在OA、OD上,且OE=
已知:如图,矩形ABCD中,对角线AC与BD交于点O,点E、F分别在OA、OD上,且OE=