题目内容
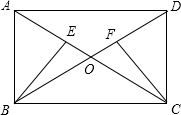 已知:如图,矩形ABCD中,对角线AC与BD交于点O,点E、F分别在OA、OD上,且OE=
已知:如图,矩形ABCD中,对角线AC与BD交于点O,点E、F分别在OA、OD上,且OE=| 1 |
| 3 |
| 1 |
| 3 |
分析:先根据矩形的性质得到OB=OC=OA=OD.再根据OE=
OA,OF=
OD,求得OE=OF.所以△BOE≌△COF,根据全等的性质可知BE=CF.
| 1 |
| 3 |
| 1 |
| 3 |
解答:证明:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=
AC,OB=OD=
BD.
∴OB=OC=OA=OD.
∵OE=
OA,OF=
OD,
∴OE=OF.
在△BOE和△COF中,
∴△BOE≌△COF.
∴BE=CF.
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB=OC=OA=OD.
∵OE=
| 1 |
| 3 |
| 1 |
| 3 |
∴OE=OF.
在△BOE和△COF中,
|
∴△BOE≌△COF.
∴BE=CF.
点评:本题考查矩形的性质和三角形全等的判定,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
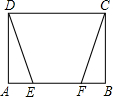 已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.
已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.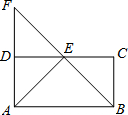 19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.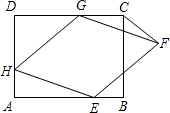 上,AH=2,连接CF.
上,AH=2,连接CF.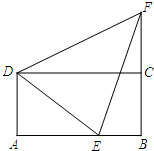 已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.
已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.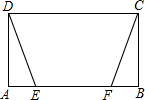 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.