摘要:已知抛物线y=ax2+bx+c在平面直角坐标系中的位置如图所示.则下列结论中.正确的是( ) A.a>0 B.b<0 C.c<0 D.a+b+c>0 考点:二次函数图象与系数的关系. 专题:数形结合. 分析:根据抛物线的开口方向判断a的正负,根据对称轴在y轴的右侧.得到a.b异号.可判断b的正负,根据抛物线与y轴的交点为(0.c).判断c的正负,由自变量x=1得到对应的函数值为正.判断a+b+c的正负. 解答:解:∵抛物线的开口向下. ∴a<0, 又∵抛物线的对称轴在y轴的右侧. ∴a.b异号. ∴b>0, 又∵抛物线与y轴的交点在x轴上方. ∴c>0. 又x=1.对应的函数值在x轴上方. 即x=1.y=ax2+bx+c=a+b+c>0, 所以A.B.C选项都错.D选项正确. 故选D. 点评:本题考查了抛物线y=ax2+bx+c中各系数的作用:a>0.开口向上.a<0.开口向下,对称轴为x=﹣.a.b同号.对称轴在y轴的左侧,a.b异号.对称轴在y轴的右侧,抛物线与y轴的交点为(0.c).c>0.与y轴正半轴相交,c<0.与y轴负半轴相交,c=0.过原点.
网址:http://m.1010jiajiao.com/timu3_id_435730[举报]
 (2013•桐乡市一模)如图,已知抛物线y=ax2+bx+c(a>0)的顶点坐标为(2,-3),将此抛物线在x轴下方的部分沿x轴往上翻折,得到一个新的函数图象(即图中的实线型图象).若|ax2+bx+c|=k(k≠0)时,对应的x的值是两个不相等的实数,则常数k的取值范围是
(2013•桐乡市一模)如图,已知抛物线y=ax2+bx+c(a>0)的顶点坐标为(2,-3),将此抛物线在x轴下方的部分沿x轴往上翻折,得到一个新的函数图象(即图中的实线型图象).若|ax2+bx+c|=k(k≠0)时,对应的x的值是两个不相等的实数,则常数k的取值范围是k>3
k>3
.已知抛物线y=ax2+bx+c(a>0)与x轴分别交于(-1,0),(5,0)两点,当自变量x=1时,函数值为y1;当x=3,函数值为y2.下列结论正确的是( )
| A、y1>y2 | B、y1=y2 | C、y1<y2 | D、不能确定 |
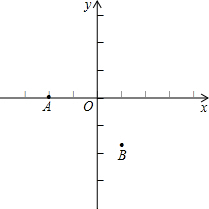 (2013•泸州)如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,-
(2013•泸州)如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,- 如图,已知抛物线
如图,已知抛物线