摘要：如图.AB为⊙O的直径.点C在⊙O上.∠A=30°.则∠B的度数为( ) A.15° B.30° C.45° D.60° 考点:圆周角定理. 分析:根据直径所对的圆周角为90°.可得∠C的度数.再利用三角形内角和定理进行计算． 解答:解:∵AB为⊙O的直径. ∴∠C=90°. ∵∠A=30°. ∴∠B=180°﹣90°﹣30°=60°． 故选D． 点评:此题主要考查了圆周角定理和三角形内角和定理.题目比较简单．
网址：http://m.1010jiajiao.com/timu3_id_435673[举报]
14、如图，AB为⊙O的直径，诸角p，q，r，s之间的关系（1）p=2q；（2）q=r；（3）p+s=180°中，正确的是（ ）如图，AB为⊙O的直径，C为⊙O上一点，AC平分∠BAD，CD⊥AD．
（1）CD是⊙O的切线吗？为什么？
（2）若AD=4，AB=9，求AC的长．
（3）若AD交⊙O于点E，连接OD交AC于点F，且
=
，求
的值．
查看习题详情和答案>>
（1）CD是⊙O的切线吗？为什么？
（2）若AD=4，AB=9，求AC的长．
（3）若AD交⊙O于点E，连接OD交AC于点F，且
| AE |
| ED |
| 3 |
| 2 |
| OF |
| DF |
如图，AB为⊙O的直径，弦CD⊥AB于点M，过点B作BE∥CD，交AC的延长线于点E，连接BC．
已知：如图，AB为⊙O的直径，AD为弦，∠DBC=∠A．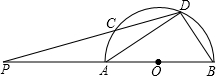
已知如图，AB为半圆的直径，C、D为半圆弧上的两点，若弧CD=弧BD，DC与BA的延长线交于P，如果，AP：CP=3：4，△ADB的面积为