摘要：7．能沿x周轴正向:Eq+Bqv=mg,能沿x周轴负向:Eq=mg+Bqv, 能沿y轴正向或负向:Eq=mg,不能沿z轴.因为电场力和重力的合力沿z轴方向.洛伦兹力沿x轴方向.合力不可能为零. 8．
网址：http://m.1010jiajiao.com/timu3_id_1624891[举报]
如图所示为一个平面直角坐标系xoy。在第Ⅰ象限中，取一个与两个坐标轴相切的圆，圆心为点D，切点为A、B，图中只画出圆的四分之一。在第Ⅱ、Ⅲ象限过M点有一条垂直x轴的虚线，其左侧固定两带电平行金属板P、Q，两板间距离为d，其中心轴线与x轴重合，板右端有挡板，只在中心轴上开有小孔。在平面直角坐标系xoy的整个空间区域中（设为真空）存在匀强磁场，磁场方向垂直于纸面向里（图中没有画出），磁感应强度的大小为B。在平行板内x轴上的S点，有一个能沿x轴正向发射相同速度粒子的粒子源，粒子的质量为m、电荷量为q（不计粒子的重力）。当调节PQ两板间的电压为
时，粒子打到挡板上距P极板为
的N点，当调节PQ两板间的电压为
时，粒子沿x轴从小孔M点射出。从小孔M射出的粒子，在磁场中做圆周运动时恰好经过AB段圆弧的中点C，且OM=OB（忽略电磁场间的相互影响）。求：
（1）粒子打到N点时的动能Ek
（2）圆弧ACB的半径R。
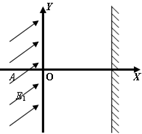如图，设在地面上方的真空室内，建立平面直角坐标系，在x＜0的空间内有倾斜方向的匀强电场，电场强度为E1，在x=0.2m处有一与X轴垂直的荧光屏．一质量为m=4×10-7kg，带电量q=1×10-5C的带电粒子（重力不能忽略）从坐标为（-| 1 |
| 15 |
（1）求E1的大小和方向（方向角可用角的三角函数值表示）
（2）粒子打在荧光屏M点，求M点的坐标．
（3）若在x＞0区域加竖直向上的匀强电场，场强E2=0.4N/C，且在如图平面内以坐标为（0.1m，0）的C点为圆心，半径为0.1m的圆形区域内有垂直于纸面的匀强磁场，粒子会打在荧光屏上坐标为（0.2m，0.1
| 3 |
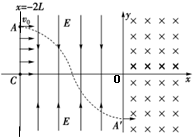如图所示的直角坐标系中，第Ⅰ、Ⅳ象限内存在着垂直纸面向里的匀强磁场，在x=-2L与y轴之间第Ⅱ、Ⅲ象限内存在大小相等，方向相反的匀强电场，场强方向如图所示．在A（-2L，L）到C（-2L，0）的连线上连续分布着电荷量为+q、质量为m的粒子．从t=0时刻起，这些带电粒子依次以相同的速度v0沿x轴正方向射出．从A点射出的粒子刚好沿如图所示的运动轨迹（轨迹与x轴的交点为OC的中点）从y轴上A′（0，-L）沿x轴正方向进入磁场．不计粒子的重力及它们间的相互作用，不考虑粒子间的碰撞．（1）求电场强度E的大小；
（2）若匀强磁场的磁感应强度B=
| 8mv0 | 5qL |
（3）在AC间还有哪些位置的粒子，经过电场后也能沿x轴正方向进入磁场．
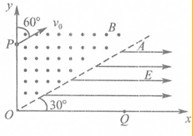如图所示，在xoy坐标系中有虚线OA，OA与x轴的夹角θ=30°，（OA与y轴之间的区域有垂直纸面向外的匀强磁场，OA与x轴之间的区域有沿x轴正方向的匀强电场，已知匀强磁场的磁感应强度B=0.25T，匀强电场的电场强度E=5×105N/C．现从y轴上的P点沿与y轴正向夹角60°的方向以初速度v0=5×105m/s射入一个质量m=8×10-26kg、电量q=+8×10-19C的带电粒子，粒子经过磁场、电场后最终打在x轴上的Q点，已知P点到O的距离为
| ||
| 5 |
（1）粒子在磁场中做圆周运动的半径；
（2）粒子从P点运动到Q点的时间；
（3）Q点的坐标．
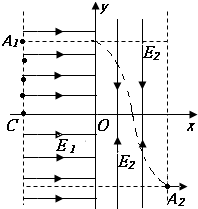如图所示的直角坐标系中，在直线x=-d到y轴区域内存在着水平向右的匀强电场E1；在直线x=d到y轴区域存在着两个大小均为E2、方向相反的有界匀强电场，其中x轴上方的电场方向沿y轴负方向，x轴下方的电场方向沿y轴正方向．在电场左边界上A1（-d，d）到C（-d，0）区域内，连续分布着电量为+q、质量为m的粒子，且均处于静止状态．若处于A1点的粒子，在电场力作用下，能恰好从右边电场的边界A2（d，-d）处沿x轴正方向射出电场，其轨迹如图．不计粒子的重力及它们间的相互作用：（1）匀强电场的电场强度E1与E2之比；
（2）在A1C间还有哪些位置的粒子，通过电场后也能沿x轴正方向运动．