题目内容
如图所示为一个平面直角坐标系xoy。在第Ⅰ象限中，取一个与两个坐标轴相切的圆，圆心为点D，切点为A、B，图中只画出圆的四分之一。在第Ⅱ、Ⅲ象限过M点有一条垂直x轴的虚线，其左侧固定两带电平行金属板P、Q，两板间距离为d，其中心轴线与x轴重合，板右端有挡板，只在中心轴上开有小孔。在平面直角坐标系xoy的整个空间区域中（设为真空）存在匀强磁场，磁场方向垂直于纸面向里（图中没有画出），磁感应强度的大小为B。在平行板内x轴上的S点，有一个能沿x轴正向发射相同速度粒子的粒子源，粒子的质量为m、电荷量为q（不计粒子的重力）。当调节PQ两板间的电压为
时，粒子打到挡板上距P极板为
的N点，当调节PQ两板间的电压为
时，粒子沿x轴从小孔M点射出。从小孔M射出的粒子，在磁场中做圆周运动时恰好经过AB段圆弧的中点C，且OM=OB（忽略电磁场间的相互影响）。求：
（1）粒子打到N点时的动能Ek
（2）圆弧ACB的半径R。
【试题解析】
（1）设粒子的初速度为v0，粒子从S点到N点时有：
（3分）
当PQ两板的电压为时：
（2分） 得：
（1分）
代入得：
（2分）
（2）解法一：粒子在磁场中做圆周运动，由洛仑兹力和牛顿运动定律
有 
（2分）得： 
（1分）
粒子做圆周运动的圆心必在过M点并垂直于x轴的直线ME上；同时这个轨迹经过C点，所以轨迹的圆心也一定在MC的垂直平分线EF上，这样ME与EF的交点E就是轨迹的圆心，ME就是轨迹的半径r。过C点作MB的垂线与MB交于H点，则△MEF∽△CMH
有：
（2分）
由 ∠CDB=45°
得CH=OD-OC
45° （1分）
MH
（1分）
（1分）
MF
MC
联立可得：
（2分）
解法二：粒子在磁场中做圆周运动，由牛顿运动定律有
（2分）
得到：
（1分）
粒子做圆周运动的圆心必在过M点并垂直于x轴的直线ME上；同时这个轨迹经过C点，所以轨迹的圆心也一定在MC的垂直平分线EF上，这样ME与EF的交点E就是轨迹的圆心，ME就是轨迹的半径r。过C点作MB的垂线与MB交于H点。
圆的轨迹方程为：
（3分）
C点坐标为：
（1分）
（1分）
代入圆的轨迹方程得：
（2分）
【参考答案】 
如图所示是一个竖直平面内的由倾斜直线、半径R=50cm圆弧和竖直直线三部分组成的带有凹槽的光滑轨道，且轨道的圆弧部分与倾斜部分恰好相切连接，倾斜轨道与水平面的夹角为45°．两个质量均为m=2kg的小环套在光滑轨道上，小环之间用不计质量且不可拉伸的细线相连（图中虚线表示），细线只能沿轨道的凹槽运动．开始时，让A、B两小环分别静止在圆弧轨道的最低点和倾斜轨道上，细线处于拉紧状态．释放后两小环开始运动，求：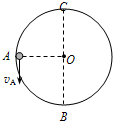
如图所示为一竖直平面内的光滑圆轨道，O是其圆心，A是轨道上与圆心等高的点，B是最低点，C是最高点，圆的半径为0.4m．有一个质量m=1kg的小球在此圆轨道的内侧运动，小球经过A点时的速率为
．筒内壁光滑，与中心轴的夹角为
＝53°，筒口半径为R＝0.6 m．现有一质量为m的小物块A在筒内壁绕中心轴作匀速圆周运动．求当物块在高度为筒高一半的平面内运动时的角速度；g＝10 m/s2
m/s．则下列判定正确的是(取g＝10 m/s2)
