摘要：15． 舟垂直于江岸时.时间最短.最短的时间为t=d/v2=5(s) (2)战士要想到达江岸的过程中航程最短.则要求合速度的方向垂直于江岸.舟头必须斜向上.设与江岸的夹角为θ.则COSθ=v1/v2=O．5 θ=600 (3)在v1>v2的条件下.舟只能斜向下游到江岸.此时v2所有可能的方向如图3所示.v与v2垂直时θ角最大.位移最短.此时sinθ=v2/v1=o．5,则θ=300.最短位移为s=50/sin300=100(m)
网址：http://m.1010jiajiao.com/timu3_id_1574315[举报]
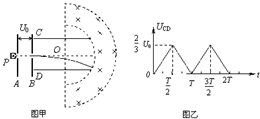如图甲所示，竖直放置的金属板A、B中间开有小孔，小孔的连线沿水平放置的金属板C、D的中轴线，粒子源P可以连续地产生质量为m、电荷量为q的带正电粒子（初速不计），粒子在A、B间被加速后，再进入金属板C、D间偏转并均能从此电场中射出．已知金属板A、B间的电压UAB=U0，金属板C、D长度为L，间距d=
| ||
| 3 |
| ||
| 3 |
|
（1）求粒子离开偏转电场时，在垂直于板面方向偏移的最大距离；
（2）若所有粒子均不能从环形磁场的右侧穿出，求环形带磁场的最小宽度．
（2010?徐州三模）如图甲所示，竖直放置的金属板A、B中间开有小孔，小孔的连线沿水平放置的金属板C、D的中间线，粒子源P可以间断地产生质量为m、电荷量为q的带正电粒子（初速不计），粒子在A、B间被加速后，再进入金属板C、D间偏转并均能从此电场中射出．已知金属板A、B间的电压UAB=U0，金属板C、D长度为L，间距d=
．两板之间的电压UCD随时间t变化的图象如图乙所示．在金属板C、D右侧有二个垂直纸面向里的均匀磁场分布在图示的半环形带中，该环带的内、外圆心与金属板C、D的中心O点重合，内圆半径Rl
=，磁感应强度B0=
．已知粒子在偏转电场中运动的时间远小于电场变化的周期（电场变化的周期T未知），粒子重力不计．
（1）求粒子离开偏转电场时，在垂直于板面方向偏移的最大距离；
（2）若所有粒子均不能从环形磁场的右侧穿出，求环带磁场的最小宽度；
（3）若原磁场无外侧半圆形边界且磁感应强度B按如图丙所示的规律变化，设垂直纸面向里的磁场方向为正方向．t=
时刻进入偏转电场的带电微粒离开电场后进入磁场，t=
时该微粒的速度方向恰好竖直向上，求该粒子在磁场中运动的时间为多少？
查看习题详情和答案>>
| ||
| 3 |
| ||
| 3 |
|
（1）求粒子离开偏转电场时，在垂直于板面方向偏移的最大距离；
（2）若所有粒子均不能从环形磁场的右侧穿出，求环带磁场的最小宽度；
（3）若原磁场无外侧半圆形边界且磁感应强度B按如图丙所示的规律变化，设垂直纸面向里的磁场方向为正方向．t=
| T |
| 2 |
| 3T |
| 4 |
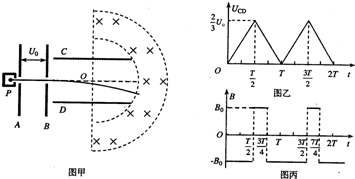
(20分)如图甲所示，竖直放置的金属板A、B中间开有小孔，小孔的连线沿水平放置的金属板C、D的中间线，粒子源P可以间断地产生质量为m、电荷量为q的带正电粒子(初速不计)，粒子在A、B间被加速后，再进入金属板C、D间偏转并均能从此电场中射出。已知金属板A、B间的电压UAB=U0，金属板C、D长度为L，间距d=
L/3。两板之间的电压UCD随时间t变化的图象如图乙所示。在金属板C、D右侧有一个垂直纸面向里的均匀磁场分布在图示的半环形带中，该环带的内、外圆心与金属板C、D的中心O点重合，内圆半径Rl=L/3，磁感应强度B0=
。已知粒子在偏转电场中运动的时间远小于电场变化的周期(电场变化的周期T未知)，粒子重力不计。
(1)求粒子离开偏转电场时，在垂直于板面方向偏移的最大距离。
(2)若所有粒子均不能从环形磁场的右侧穿出，求环带磁场的最小宽度。
(3)若原磁场无外侧半圆形边界且磁感应强度B按如图丙所示的规律变化，设垂直纸面向里的磁场方向为正方向。t=T/2时刻进入偏转电场的带电微粒离开电场后进入磁场，t=3T/4时该微粒的速度方向恰好竖直向上，求该粒子在磁场中运动的时间为多少?
查看习题详情和答案>>