题目内容
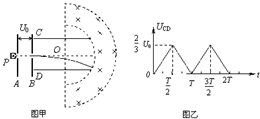 如图甲所示,竖直放置的金属板A、B中间开有小孔,小孔的连线沿水平放置的金属板C、D的中轴线,粒子源P可以连续地产生质量为m、电荷量为q的带正电粒子(初速不计),粒子在A、B间被加速后,再进入金属板C、D间偏转并均能从此电场中射出.已知金属板A、B间的电压UAB=U0,金属板C、D长度为L,间距d=
如图甲所示,竖直放置的金属板A、B中间开有小孔,小孔的连线沿水平放置的金属板C、D的中轴线,粒子源P可以连续地产生质量为m、电荷量为q的带正电粒子(初速不计),粒子在A、B间被加速后,再进入金属板C、D间偏转并均能从此电场中射出.已知金属板A、B间的电压UAB=U0,金属板C、D长度为L,间距d=
| ||
| 3 |
| ||
| 3 |
|
(1)求粒子离开偏转电场时,在垂直于板面方向偏移的最大距离;
(2)若所有粒子均不能从环形磁场的右侧穿出,求环形带磁场的最小宽度.
分析:(1)对粒子加速过程由动能定理求得进入偏转电场的速度.要在垂直于板面方向偏移的距离最大,那么粒子的加速度也要最大,即所加的电压最大.根据类平抛运动的规律求解.
(2)进入偏转电场的粒子刚好不能穿出磁场时的环带宽度为磁场的最小宽度,根据动能定理求出粒子进入磁场时的速度,画出粒子刚好不能穿出磁场的轨迹图,根据半径公式结合几何关系求解.
(2)进入偏转电场的粒子刚好不能穿出磁场时的环带宽度为磁场的最小宽度,根据动能定理求出粒子进入磁场时的速度,画出粒子刚好不能穿出磁场的轨迹图,根据半径公式结合几何关系求解.
解答: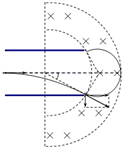 解:(1)设粒子进入偏转电场瞬间的速度为v,
解:(1)设粒子进入偏转电场瞬间的速度为v,
对粒子加速过程由动能定理得qUAB=
m
进入偏转电场后,加速度a=
设运动时间为t,则有L=v0t
只有t=
时刻进入偏转电场的粒子,垂直于极板方向偏移的距离最大
y=
at2=
=
L
(2)t=
时刻进入偏转电场的粒子刚好不能穿出磁场时的环带宽度为磁场的最小宽度.
设粒子进入磁场时的速度为v′,
对粒子的偏转过程有
qU=
mv′2-
mv2
解得:v′=
在磁场中做圆周运动的半径为R=
=
如图所示,设环带外圆半径为R2,
(R2-R1)2=
解得:R2=L
所求d=R2-R1=(1-
)L
答:(1)粒子离开偏转电场时,在垂直于板面方向偏移的最大距离是
L;
(2)环形带磁场的最小宽度是(1-
)L.
 解:(1)设粒子进入偏转电场瞬间的速度为v,
解:(1)设粒子进入偏转电场瞬间的速度为v,对粒子加速过程由动能定理得qUAB=
| 1 |
| 2 |
| v | 2 |
进入偏转电场后,加速度a=
| qUcd |
| md |
设运动时间为t,则有L=v0t
只有t=
| T |
| 2 |
y=
| 1 |
| 2 |
| qUcd |
| md |
| ||
| 6 |
(2)t=
| T |
| 2 |
设粒子进入磁场时的速度为v′,
对粒子的偏转过程有
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v′=
|
在磁场中做圆周运动的半径为R=
| mv |
| qB |
| L |
| 3 |
如图所示,设环带外圆半径为R2,
(R2-R1)2=
| R | 2 1 |
| +R | 2 2 |
解得:R2=L
所求d=R2-R1=(1-
| ||
| 3 |
答:(1)粒子离开偏转电场时,在垂直于板面方向偏移的最大距离是
| ||
| 6 |
(2)环形带磁场的最小宽度是(1-
| ||
| 3 |
点评:本题主要考查了带电粒子分别在电场和磁场中的运动情况,当两极间加上电压时,粒子做类平抛运动,根据类平抛运动规律求解问题.粒子在匀强磁场中的运动,要掌握住半径公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
相关题目
 (2009?徐汇区模拟)如图甲所示,竖直放置的汽缸内壁光滑,活塞厚度与质量均不计,在B处设有限制装置,使活塞只能在B以上运动,B以下汽缸的容积为V0,A、B之间的容积为0.2V0.开始时活塞在A处,温度为87℃,大气压强为p0,现缓慢降低汽缸内气体的温度,直至活塞移动到A、B的正中间,然后保持温度不变,在活塞上缓慢加砂,直至活塞刚好移动到B,然后再缓慢降低汽缸内气体的温度,直到-3℃.求:
(2009?徐汇区模拟)如图甲所示,竖直放置的汽缸内壁光滑,活塞厚度与质量均不计,在B处设有限制装置,使活塞只能在B以上运动,B以下汽缸的容积为V0,A、B之间的容积为0.2V0.开始时活塞在A处,温度为87℃,大气压强为p0,现缓慢降低汽缸内气体的温度,直至活塞移动到A、B的正中间,然后保持温度不变,在活塞上缓慢加砂,直至活塞刚好移动到B,然后再缓慢降低汽缸内气体的温度,直到-3℃.求: (2013?松江区一模)如图甲所示,竖直放置的无限长直导线的右侧固定一小圆环,直导线与小圆环在同一平面内,导线中通入如图乙所示电流,(规定电流方向向上时为正)下列说法正确的是( )
(2013?松江区一模)如图甲所示,竖直放置的无限长直导线的右侧固定一小圆环,直导线与小圆环在同一平面内,导线中通入如图乙所示电流,(规定电流方向向上时为正)下列说法正确的是( ) 如图甲所示,竖直放置的长直导线MN通有图示方向的恒定电流I,有一闭合矩形金属框abcd与导线在同一平面内,在金属框内部通有如图乙所示的变化磁场(规定垂直于纸面向里为磁场的正方向),下列说法正确的是( )
如图甲所示,竖直放置的长直导线MN通有图示方向的恒定电流I,有一闭合矩形金属框abcd与导线在同一平面内,在金属框内部通有如图乙所示的变化磁场(规定垂直于纸面向里为磁场的正方向),下列说法正确的是( )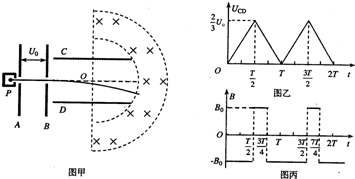
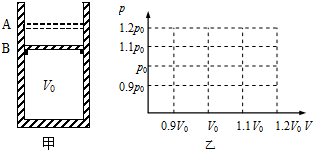 如图甲所示,竖直放置的汽缸内壁光滑,活塞厚度与质量均不计,在B处设有限制装置,使活塞只能在B以上运动,B以下汽缸的容积为V0,A、B之间的容积为0.2V0.开始时活塞在B处,缸内气体的压强与大气压强p0相同,温度为77°C,现缓慢升高汽缸内气体的温度,直至活塞移动到A处,然后保持温度不变,在活塞上缓慢加砂,直至活塞刚好移动到B,然后再缓慢降低汽缸内气体的温度,直到42°C.求:
如图甲所示,竖直放置的汽缸内壁光滑,活塞厚度与质量均不计,在B处设有限制装置,使活塞只能在B以上运动,B以下汽缸的容积为V0,A、B之间的容积为0.2V0.开始时活塞在B处,缸内气体的压强与大气压强p0相同,温度为77°C,现缓慢升高汽缸内气体的温度,直至活塞移动到A处,然后保持温度不变,在活塞上缓慢加砂,直至活塞刚好移动到B,然后再缓慢降低汽缸内气体的温度,直到42°C.求: