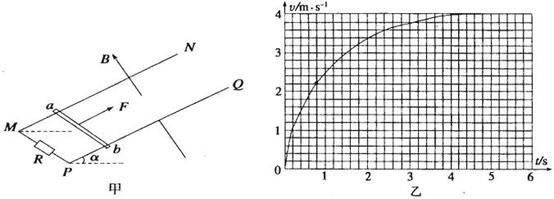
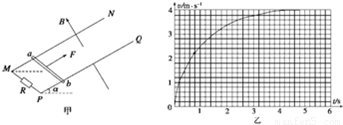
摘要：20．光滑平行的金属导轨MN和PQ.间距L＝1.0 m.与水平面之间的夹角α＝30°.匀强磁场磁感应强度B＝2.0 T.垂直于导轨平面向上.MP间接有阻值R＝2.0 Ω的电阻.其他电阻不计.质量m＝2.0 kg的金属杆ab垂直导轨放置.如图(甲)所示．用恒力F沿导轨平面向上拉金属杆ab.由静止开始运动.vt图象如图(乙)．g＝10 m/s2.导轨足够长.求: (1)恒力F的大小, (2)金属杆速度为2.0 m/s时的加速度大小, (3)根据vt图象估算在前0.8 s内电阻上产生的热量． 答案:2.0 m/s2 (3)3.80 J 解析:知.杆运动的最大速度为vm＝4 m/s 此时有:F＝mgsin α+F安 ＝mgsin α+ 代入数据得:F＝18 N (2)由牛顿第二定律可得:F-F安-mgsin α＝ma a＝.代入数据得:a＝2.0 m/s2 图可知0.8 s末导体杆的速度v1＝2.2 m/s 前0.8 s内图线与t轴所包围的小方格的个数为27个.面积为27×0.2×0.2＝1.08.即前0.8 s内导体杆的位移x＝1.08 m．由能的转化和守恒定律得: Q＝Fx-mgxsin α-mv12.代入数据得:Q＝3.80 J (说明.前0.8 s内图线与t轴所包围的小方格的个数在26-28个之间.位移在1.04-1.12 m之间.产生的热量在3.48-4.12 J之间均正确)．
网址：http://m.1010jiajiao.com/timu3_id_1393460[举报]
光滑平行的金属导轨MN和PQ，间距为L，导轨平面与水平面之间的夹角为α，匀强磁场磁感应强度为B，方向垂直于导轨平面向上，MP间接有阻值为R的电阻，其他电阻不计，质量为m的金属杆ab垂直导轨放置并与导轨接触良好，如图甲所示．现用恒力F沿导轨平面向上拉金属杆ab，ab由静止开始运动，vt图象如图乙所示．设导轨足够长，题中L、α、B、R、m及重力加速度g均为己知，则下列说法中正确的是（ ）
查看习题详情和答案>>
光滑平行的金属导轨MN和PQ，间距L=1.0m，与水平面之间的夹角α=30°，匀强磁场磁感应强度B=2.0T，垂直于导轨平面向上，MP间接有阻值R=2.0Ω的电阻，其它电阻不计，质量m=2.0kg的金属杆ab垂直导轨放置，如图甲所示。用恒力F沿导轨斜面向上拉金属杆ab，由静止开始运动，v―t图像如图乙。g=10m/s2，导轨足够长，求：
（1）恒力F的大小；
（2）金属杆速度为2.0m/s时的加速度大小；
（3）根据v―t图像估算在前0.8s内电阻上产生的热量。
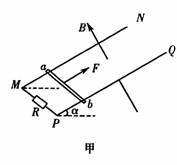
（18分）光滑平行的金属导轨MN和PQ，间距L=1.0m，与水平面之间的夹角
=300，匀强磁场磁感应强度B=2.0 T，垂直于导轨平面向上，MP间接有阻值R=2.0
的电阻，其它电阻不计，质量m=2.0 kg的金属杆ab垂直导轨放置，如图甲所示．用恒力F沿导轨平面向上拉金属杆ab，由静止开始运动，v—t图象如图乙所示，g = 10 m／s2,导轨足够长．求：
（1）恒力F的大小．
（2）金属杆速度为2.0 m/s时的加速度大小．
=300，匀强磁场磁感应强度B=2.0 T，垂直于导轨平面向上，MP间接有阻值R=2.0
的电阻，其它电阻不计，质量m=2.0 kg的金属杆ab垂直导轨放置，如图甲所示．用恒力F沿导轨平面向上拉金属杆ab，由静止开始运动，v—t图象如图乙所示，g = 10 m／s2,导轨足够长．求：
