摘要：13．“翻滚过山车 的物理原理可以用如图所示装置演示.光滑斜槽轨道AD与半径为R＝0.1 m的竖直圆轨道(圆心为O)相连.AD与圆O相切于D点.B为轨道的最低点.∠DOB＝37°.质量为m＝0.1 kg的小球从距D点L＝1.3 m处由静止开始下滑.然后冲上光滑的圆形轨道(g＝10 m/s2.sin37°＝0.6.cos37°＝0.8)．求: (1)小球在光滑斜槽轨道上运动的加速度的大小, (2)小球通过B点时对轨道的压力的大小, (3)试分析小球能否通过竖直圆轨道的最高点C.并说明理由． [答案] (1)6m/s2 能 [解析] (1)在光滑斜槽上由牛顿第二定律得: mgsin37°＝ma. 故a＝gsin37°＝6m/s2 (2)小球由A至B.机械能守恒.则 mg(Lsin37°+hDB)＝mv hDB＝R 又小球在B点.由牛顿第二定律得: FNB＝mg+m＝17N 由牛顿第三定律得:小球过B点时对轨道的压力大小为17N. (3)小球要过最高点.需要的最小速度为v0 则mg＝m 即v0＝＝1m/s 又小球从A到C机械能守恒.所以 mg[Lsin37°-R]＝mv 解之vC＝m/s>1m/s 故小球能过最高点C.
网址：http://m.1010jiajiao.com/timu3_id_1391567[举报]
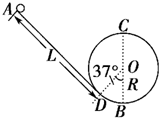“翻滚过山车”的物理原理可以用如图所示装置演示．光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道（圆心为O）相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB=37°．质量为m=0.1kg的小球从距D点L=1.3m处静止开始下滑，然后冲上光滑的圆形轨道（g=10m/s2，sin37°=0.6，cos37°=0.8）．求：（1）小球在光滑斜槽轨道上运动和加速度的大小；
（2）小球通过B点时对轨道的压力大小；
（3）试分析小球能否通过竖直圆轨道的最高点C，并说明理由．
“翻滚过山车”的物理原理可以用如图
所示装置演示，光滑斜槽轨道AD与半径为R＝0.1m的竖直圆轨道(圆心为O)相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB＝37°.质量为m＝0.1kg的小球从距D点L＝1.3m处由静止开始下滑，然后冲上光滑的圆形轨道(g＝10m/s2，sin37°＝0.6，cos37°＝0.8)．求：
(1)小球在光滑斜槽轨道上运动的加速度的大小；
(2)小球通过B点时对轨道的压力的大小；
(3)试分析小球能否通过竖直圆轨道的最高点C，并说明理由．
所示装置演示，光滑斜槽轨道AD与半径为R＝0.1m的竖直圆轨道(圆心为O)相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB＝37°.质量为m＝0.1kg的小球从距D点L＝1.3m处由静止开始下滑，然后冲上光滑的圆形轨道(g＝10m/s2，sin37°＝0.6，cos37°＝0.8)．求：(1)小球在光滑斜槽轨道上运动的加速度的大小；
(2)小球通过B点时对轨道的压力的大小；
(3)试分析小球能否通过竖直圆轨道的最高点C，并说明理由．
“翻滚过山车”的物理原理可以用如图所示装置演示。光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道（圆心为O）相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB=37°。质量为m=0.1kg的小球从距D点L=1.3m处静止开始下滑，然后冲上光滑的圆形轨道（g取10m/s2,sin37°=0.6，cos37°=0.8）。求：
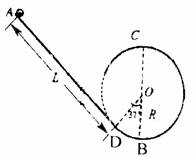
（1）小球通过B点时对轨道的压力大小；
（2）试分析小球能否通过竖直圆轨道的最高点C，并说明理由。
查看习题详情和答案>>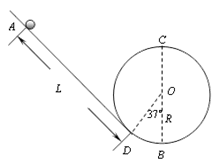
）。求：
（1）小球在光滑斜槽轨道上运动的加速度的大小；
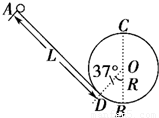“翻滚过山车”的物理原理可以用如图所示装置演示．光滑斜槽轨道AD与半径为R=0.1m的坚直圆轨道（圆心为O）相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB=37°．质量为m=0.1kg的小球从距D点L=1.3m处静止开始下滑，然后冲上光滑的圆形轨道（g=10m/s2，sin37°=0.6，cos37°=0.8）．