题目内容
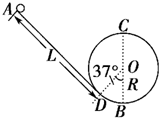 “翻滚过山车”的物理原理可以用如图所示装置演示.光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AD与圆O相切于D点,B为轨道的最低点,∠DOB=37°.质量为m=0.1kg的小球从距D点L=1.3m处静止开始下滑,然后冲上光滑的圆形轨道(g=10m/s2,sin37°=0.6,cos37°=0.8).
“翻滚过山车”的物理原理可以用如图所示装置演示.光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AD与圆O相切于D点,B为轨道的最低点,∠DOB=37°.质量为m=0.1kg的小球从距D点L=1.3m处静止开始下滑,然后冲上光滑的圆形轨道(g=10m/s2,sin37°=0.6,cos37°=0.8).求:(1)小球在光滑斜槽轨道上运动和加速度的大小;
(2)小球通过B点时对轨道的压力大小;
(3)试分析小球能否通过竖直圆轨道的最高点C,并说明理由.
分析:(1)根据牛顿第二定律列式即可求出小球在光滑斜槽上运动的加速度.
(2)根据机械能守恒定律列式求解出B点的速度,在B点,根据重力和支持力的合力提供向心力列式求解;
(3)先求出小球能到最高点的临界速度,然后根据机械能守恒定律列式求解实际速度进行比较即可判断.
(2)根据机械能守恒定律列式求解出B点的速度,在B点,根据重力和支持力的合力提供向心力列式求解;
(3)先求出小球能到最高点的临界速度,然后根据机械能守恒定律列式求解实际速度进行比较即可判断.
解答:解:(1)由牛顿第二定律F=ma可知:
mgsin37°=ma…①
故a=gsin37°=6m/s2
(2)小球由A到B的过程中只有重力做功,符合机械能守恒.选B点为重力势能的零点,即
mg(Lsin37°+hDB)=
m
…②
其中hDB=R(1-cos37°)…③
在B处,由牛顿第二定律F=ma
即NB-mg=m
…④
联立②③④可得NB=mg+m
…⑤
将已知条件代入上式得NB=17N
由牛顿第三定律可知:小球通过B点时对轨道的压力大小为17N.
(3)小球在竖直平面由沿轨道做圆周运动,通过最高点的最小速度设为v0
则有mg=m
得 v0=
=1m/s…⑥
小球从A点由静止开始滑下到达最高点C,此过程只有重力对小球做功,故机械能守恒.选C点为重力势能的零点,
则有mg[Lsin37°-R(1+cos37°)]=
m
…⑤
求得vC=
m/s>v0
所以小球能通过轨道最高点C.
答:
(1)小球在光滑斜槽轨道上运动和加速度的大小为6m/s2.
(2)小球通过B点时对轨道的压力的大小为17N;
(3)小球能通过竖直圆轨道的最高点C.
mgsin37°=ma…①
故a=gsin37°=6m/s2
(2)小球由A到B的过程中只有重力做功,符合机械能守恒.选B点为重力势能的零点,即
mg(Lsin37°+hDB)=
| 1 |
| 2 |
| v | 2 B |
其中hDB=R(1-cos37°)…③
在B处,由牛顿第二定律F=ma
即NB-mg=m
| ||
| R |
联立②③④可得NB=mg+m
| 2g[Lsin37°+R(1-cos37°)] |
| R |
将已知条件代入上式得NB=17N
由牛顿第三定律可知:小球通过B点时对轨道的压力大小为17N.
(3)小球在竖直平面由沿轨道做圆周运动,通过最高点的最小速度设为v0
则有mg=m
| ||
| R |
得 v0=
| gR |
小球从A点由静止开始滑下到达最高点C,此过程只有重力对小球做功,故机械能守恒.选C点为重力势能的零点,
则有mg[Lsin37°-R(1+cos37°)]=
| 1 |
| 2 |
| v | 2 C |
求得vC=
| 12 |
所以小球能通过轨道最高点C.
答:
(1)小球在光滑斜槽轨道上运动和加速度的大小为6m/s2.
(2)小球通过B点时对轨道的压力的大小为17N;
(3)小球能通过竖直圆轨道的最高点C.
点评:本题关键是对小球的运动过程运用机械能守恒定律列式求解不同位置的速度,同时要结合牛顿第二定律列式判断.

练习册系列答案
相关题目
 游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB,EF与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AB,EF分别与圆O相切于B、E点,C为轨道的最低点,∠BOC=37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB,EF与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AB,EF分别与圆O相切于B、E点,C为轨道的最低点,∠BOC=37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求: 在游乐园坐过山车是一项惊险、刺激的游戏.游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB、EF与半径R=0.4m的竖直圆轨道(圆心为O)相连,AB、EF分别与圆O相切于B、E点,C为轨道的最低点,斜轨AB倾角为37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
在游乐园坐过山车是一项惊险、刺激的游戏.游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB、EF与半径R=0.4m的竖直圆轨道(圆心为O)相连,AB、EF分别与圆O相切于B、E点,C为轨道的最低点,斜轨AB倾角为37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求: