摘要: 如图所示,在边界半径为a的圆柱空间中充满磁感应强度大小为B的匀强磁场,其方向平行于轴线.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架DEF,其中心O位于圆柱的轴线上.DE边上S点有一发射带电粒子的源,发射粒子的方向皆在图中截面内且垂直于DE边向下.发射粒子的电量皆为q,质量皆为m,但速度v可以有各种不同的数值.若这些粒子与三角形框架的碰撞均为完全弹性碰撞,并要求每一次碰撞时速度方向垂直于被碰撞的边,如果从S点发出的粒子最终又回到S点.而且所用时间最短.问:(1)带电粒子速度v应取多大?(2)回到S点所用的最短时间是多少?
网址:http://m.1010jiajiao.com/timu3_id_1237392[举报]
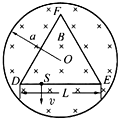 如图所示,在边界半径为a的圆柱空间中(图中圆为其横截面)充满磁感应强度大小为B的匀强磁场,其方向平行于轴线.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架DEF,其中心O位于圆柱的轴线上.DE边上S点(DS=L/4)有一发射带电粒子的源,发射粒子的方向皆在图中截面内且垂直于DE边向下.发射粒子的电量皆为q(q>0),质量皆为m,但速度v可以有各种不同的数值.若这些粒子与三角形框架的碰撞均为完全弹性碰撞,并要求每一次碰撞时速度方向垂直于被碰撞的边,如果从S点发出的粒子最终又回到S点,而且所用时间最短,问:
如图所示,在边界半径为a的圆柱空间中(图中圆为其横截面)充满磁感应强度大小为B的匀强磁场,其方向平行于轴线.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架DEF,其中心O位于圆柱的轴线上.DE边上S点(DS=L/4)有一发射带电粒子的源,发射粒子的方向皆在图中截面内且垂直于DE边向下.发射粒子的电量皆为q(q>0),质量皆为m,但速度v可以有各种不同的数值.若这些粒子与三角形框架的碰撞均为完全弹性碰撞,并要求每一次碰撞时速度方向垂直于被碰撞的边,如果从S点发出的粒子最终又回到S点,而且所用时间最短,问:(1)带电粒子速度v应取多大?
(2)回到S点所用的最短时间是多少?
 如图所示,A板和B板为平行板电容器的两极板,其中A板带负电,B板带正电,两极板的中央都有一个小空隙可以允许粒子穿过,两板间的电势差的大小为U=1×105B极板的右上方存在着一个圆心为O1圆柱形匀强磁场区域,磁感应强度B=0.1T,磁场区域半径r=
如图所示,A板和B板为平行板电容器的两极板,其中A板带负电,B板带正电,两极板的中央都有一个小空隙可以允许粒子穿过,两板间的电势差的大小为U=1×105B极板的右上方存在着一个圆心为O1圆柱形匀强磁场区域,磁感应强度B=0.1T,磁场区域半径r=| 2 |
| 3 |
| 3 |
(1)该粒子刚刚进入圆柱形匀强磁场区域时的速度大小;
(2)该粒子通过圆形磁场区域所用的时间;
(3)该粒子在有界匀强电场中的位移大小.
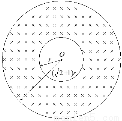
在一空心圆柱面内有一垂直于纸面的匀强磁场,磁感应强度为B,其横截面如图所示,磁场边界为同心圆,内、外半径分别为r和( )
) .圆心处有一粒子源不断地沿半径方向射出质量为
.圆心处有一粒子源不断地沿半径方向射出质量为 、电量为q的带电粒子,不计粒子重力.为使这些粒子不射出磁场外边界,粒子从圆心处射出时速度不能超过
、电量为q的带电粒子,不计粒子重力.为使这些粒子不射出磁场外边界,粒子从圆心处射出时速度不能超过
A. | B. | C. | D.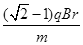 |







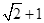 )
) .圆心处有一粒子源不断地沿半径方向射出质量为
.圆心处有一粒子源不断地沿半径方向射出质量为 、电量为q的带电粒子,不计粒子重力.为使这些粒子不射出磁场外边界,粒子从圆心处射出时速度不能超过
、电量为q的带电粒子,不计粒子重力.为使这些粒子不射出磁场外边界,粒子从圆心处射出时速度不能超过



