Question

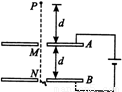
如图所示，A板和B板为平行板电容器的两极板，其中A板带负电，B板带正电，两极板的中央都有一个小空隙可以允许粒子穿过，两板间的电势差的大小为U=1×10⁵B极板的右上方存在着一个圆心为O₁圆柱形匀强磁场区域，磁感应强度B=0.1T，磁场区域半径r=

2

3

3

m，磁场的方向垂直于纸面向里．今有质量m=3.2×10^-26、带电荷量q=-1.6×10^-19某种粒子，从A极板小孔处以极小的初速度（其方向由A到B，大小可以视为零）进入两平行金属板之间的区域．图中A、B板上的两个小孔和O₁点共线．粒子穿越圆柱形磁场后恰好从磁场区域的最右端C点穿出，立即进入一个竖直方向的有界匀强电场，其左右边界分别为DE和FH，两边界间的距离为8m，上边和下边没有边界．匀强电场的场强大小为E=3.75×10⁴/C，方向在竖直方向上．试求：
（1）该粒子刚刚进入圆柱形匀强磁场区域时的速度大小；
（2）该粒子通过圆形磁场区域所用的时间；
（3）该粒子在有界匀强电场中的位移大小．

Answer 1

分析：（1）粒子在两极板中加速的过程，根据动能定理即可求出速度；
（2）粒子在磁场中做匀速圆周运动，设轨迹半径为R，圆周运动的周期为T，由牛顿第二定律求出半径，根据T=

2πR

v

求出周期，根据运动轨迹求出偏转的圆心角，进而求出运动的时间；
（3）由题意可知：该粒子进入有界匀强电场中做类平抛运动，根据平抛运动的基本公式求出水平和竖直方向的位移，根据矢量合成求出总位移．

解答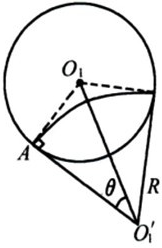：解：（1）根据动能定理得：
qU=

1

2

mv2
解得：v=

2qU m

=1.0×106m/s
（2）粒子在磁场中做匀速圆周运动，设轨迹半径为R，圆周运动的周期为T，由牛顿第二定律得：
qvB=m

v2

R

又T=

2πR

v

解得：R=

mv

Bq

=2m，
T=

2πm

Bq

由轨迹图可知：
tanθ=

r

R

=

3

3

则θ=30°
则该段轨迹的运动时间t=T?

2θ

360°

=

T

6

=2.1×10-6s
（3）由题意可知：该粒子进入有界匀强电场中做类平抛运动，
设粒子在匀强电场中运动的时间为t，则x=vt
y=

1

2

at2
再根据牛顿第二定律有：qE=ma
解得：粒子的总位移为s=

x2+y2

=10m
答：（1）该粒子刚刚进入圆柱形匀强磁场区域时的速度大小为1.0×10⁶m/s；
（2）该粒子通过圆形磁场区域所用的时间为2.1×10^-6s；
（3）该粒子在有界匀强电场中的位移大小为10m．

点评：带电粒子在电场中运动分为加速和偏转两种类型，常运用动能定理和平抛运动规律求解，注意运算时要细心，而在匀强磁场中运动时，重要的是由运动径迹利用几何关系找到半径的大小，由洛伦兹力提供向心力，利用牛顿第二定律求解即可