2009年侨声中学第一次校质检
数 学(理工类)
时间 2009-4-30 15:00??17:00
一.选择题(本大题共10小题,每小题5分,共50分. 在每小题所给的四个答案中有且只有一个答案是正确的)
1.复数 在复平面内的对应点位于 ( )
在复平面内的对应点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设 是集合A到集合B的映射,若
是集合A到集合B的映射,若 则
则 等于 ( )
等于 ( )
A.  B.
B.
 C.
C.
 或
或 D.
D.  或
或
3.下列大小关系正确的是 ( )
A.  B.
B.

 学科网
学科网
C.  D.
D.

 学科网
学科网
4.小李晨练所花时间(单位:分钟)分别为x,y,30,29,31,已知这组数据的平均数为30,方差为2,则|x-y|的值为 ( )
A.1 B.2 C.3 D.4
5. 已知命题:若 ,则
,则 成立,则字母
成立,则字母 在空间所表示的一定不是 ( )
在空间所表示的一定不是 ( )
A. 都是直线 B.
都是直线 B. 都是平面
都是平面
C. 是直线,
是直线, 是平面 D.
是平面 D. 是平面,
是平面, 是直线
是直线
6. 方程的根也可以叫做函数的零点,则函数 零点的个数为( )
零点的个数为( )
A 4 B 3 C 2 D 1

 7.点(0,3)到由曲线
7.点(0,3)到由曲线 的准线的距离为
的准线的距离为 ,则曲线
,则曲线 和直线x=1围成图形的面积是 ( )
和直线x=1围成图形的面积是 ( )
 A.3 B.
A.3 B. C.
C. D.
D.
8. 在如下图所示的坐标平面的可行域内(阴影部分且
包括边界),若目标函数 z=x+ay取得最小值的最优
解有无数个,则a等于 ( )
A.1 B. C.
C. D.
D.
9.计算机是将信息转换成二进制进行处理的. 二进制即“逢二进一”,如 表示二进制数,将它转换成十进制形式是
表示二进制数,将它转换成十进制形式是 = 13,那么将二进制数
= 13,那么将二进制数 转换成十进制形式是( ).
转换成十进制形式是( ).
A. B.
B. C.
C. D.
D.
10. 有限数列 ,
, 为其前
为其前 项和,定义
项和,定义 为
为 的“优化和”;现有2007项的数列
的“优化和”;现有2007项的数列 的“优化和”为2008,则有2008项的数列
的“优化和”为2008,则有2008项的数列 的“优化和”为( )
的“优化和”为( )
A.2007 B.2008 C.2009 D.2006
第Ⅱ卷 (非选择题 共100分)
二.填空题(本大题共5小题,每小题4分,共20分,将答案填在题后的横线上.)
11.已知向量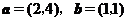 .若向量
.若向量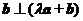 ,则实数
,则实数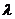 的值是
的值是
12. 在某项测量中,测量结果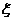 服从正态分布
服从正态分布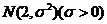 ,若
,若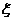 在(0,2)内取值的概率为0.4,则
在(0,2)内取值的概率为0.4,则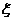 在
在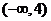 内取值的概率为
内取值的概率为
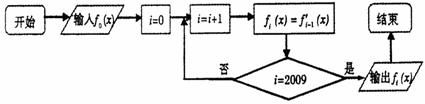
13. 在如下程序图框中,输入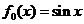 ,则输出的是
,则输出的是
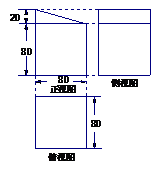
14. 某师傅需用合板制作一个工作台,工作台由
主体和附属两部分组成,主体部分全封闭,附属
部分是为了防止工件滑出台面而设置的护墙,其
大致形状的三视图如右图所示(单位长度: cm), 则
按图中尺寸,做成的工作台用去的合板的面积为
(制作过程合板损耗和合板厚度忽略不计)
15.对于集合N={1, 2,
3,…, n}的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数.例如集合{1, 2, 4, 6, 9}的交替和是9?6+4?2+1=6,集合{5}的交替和为5.当集合N中的n =2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和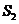 =1+2+(2?1)=4,则当
=1+2+(2?1)=4,则当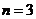 时,
时,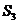 = _____ , ;根据
= _____ , ;根据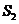 、
、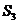 、
、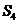 ,猜想集合N ={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和
,猜想集合N ={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和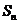 =_____
=_____
三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算过程)
16. (本小题满分13分)
已知函数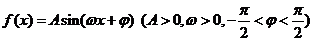 一个周期的图象如图所示,
一个周期的图象如图所示,
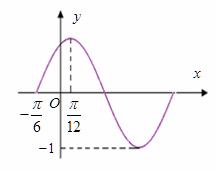 (1)求函数
(1)求函数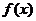 的表达式;
的表达式;
(2)若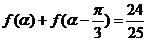 ,且
,且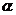 为
为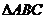 的一个内角,求
的一个内角,求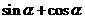 的值.
的值.
17.(本小题满分13分)
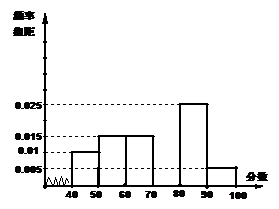 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段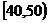 ,
,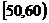 …
…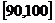 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和
平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,
求他们在同一分数段的概率.
18、(本小题满分13分)
受金融危机的影响,三峡某旅游公司经济效益出现了一定程度的滑坡.现需要对某一景点进行改造升级,从而扩大内需,提高旅游增加值. 经过市场调查,旅游增加值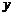 万元与投入
万元与投入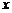 万元之间满足:
万元之间满足: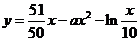 ,
,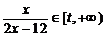 ,其中
,其中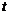 为大于
为大于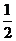 的常数.当
的常数.当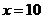 万元时
万元时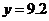 万元.
万元.
(1)求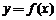 的解析式和投入
的解析式和投入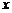 的取值范围;
的取值范围;
(2)求出旅游增加值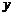 取得最大值时对应的
取得最大值时对应的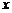 值.
值.
19. (本小题满分13分)
已知动圆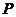 过点
过点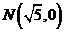 并且与圆
并且与圆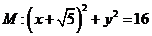 相外切,动圆圆心
相外切,动圆圆心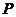 的轨迹为
的轨迹为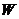 ,轨迹
,轨迹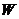 与
与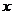 轴的交点为
轴的交点为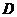 .
.
(1)求轨迹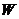 的方程;
的方程;
(2)设直线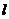 过点
过点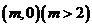 且与轨迹
且与轨迹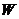 有两个不同的交点
有两个不同的交点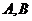 ,求直线
,求直线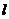 斜率
斜率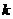 的取值范围;
的取值范围;
(3)在(Ⅱ)的条件下,若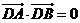 ,证明直线
,证明直线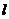 过定点,并求出这个定点的坐标.
过定点,并求出这个定点的坐标.
20.(本小题满分14分)
已知函数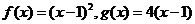 ,数列
,数列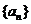 满足
满足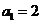 ,且
,且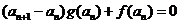 .
.
(1)试探究数列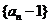 是否是等比数列?
是否是等比数列?
(2)试证明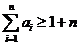 ;
;
(3)设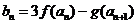 ,试探究数列
,试探究数列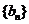 是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.
是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.
21. (本小题满分14分)
本题有(Ⅰ)、(Ⅱ)、(Ⅲ)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(Ⅰ)二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(1)求矩阵M的逆矩阵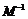 ;
;
(2)设直线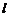 在变换M作用下得到了直线m:2x-y=4,求
在变换M作用下得到了直线m:2x-y=4,求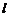 的方程.
的方程.
(Ⅱ)在极坐标系中,设圆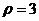 上的点到直线
上的点到直线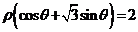 的距离为
的距离为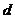 ,求
,求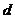 的最大值.
的最大值.
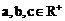 ,求证:
,求证: