3.1 数列的概念
〖考试要求〗
理解数列的概念,了解数列通项公式的意义;了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项,能熟练应用关系式: .
.
〖双基回顾〗
1、数列:
⑴定义: ;或者 .
⑵表示方法: ;或者 ;或者 .
2、数列的分类:
⑴按项数的多少分:
①有穷数列――
②无穷数列――
⑵按相邻项间的大小关系分:
①递增数列―― ②递减数列――
③常数数列―― ④摆动数列――
3、设数列{an}的前n项和为Sn=a1+a2+…+an,则当 时,an=Sn?Sn?1.
〖知识点训练〗
1、根据已知条件写出下列数列的前5项:
⑴Sn=n2+1;
⑵a1=1,an+1=an+ ;
;
⑶a1=1,a
2、数列{an}中,an=n2-7n+6,那么150是其第 项.
3、已知an+2=an+1+an,a1=1,a2=2,bn= ,则数列{bn}的前4项依次为
.
,则数列{bn}的前4项依次为
.
〖典型例题分析〗
1、根据已知条件写出下列数列的一个通项公式:
⑴2 ,4
,4 ,6
,6 ,8
,8 ,…,an=
;
,…,an=
;
⑵1 ,4
,4 ,7
,7 ,10
,10 ,…,an=
;
,…,an=
;
⑶1, ,2,
,2, ,…,an=
;
,…,an=
;
2、已知数列{an}的通项公式为an=
⑴0.98是不是它的项? ⑵判断此数列的单调性.
3、设数列{an}中,Sn=-4n2+25n+1
(1)求通项公式; (2)求a10+a11+a12+…+a20的值; (3)求Sn最大时an的值.
*4、在数列{an}中,其前n项和Sn= .试问数列有没有最大项?若有,求出最大项和最大项的项数;若没有,说明理由.
.试问数列有没有最大项?若有,求出最大项和最大项的项数;若没有,说明理由.
〖课堂小结〗
1、求数列的通项公式的常用方法有:观察法、递推法、叠加(乘)法、归纳法.
2、由Sn求an时要注意分n=1和n>1两种情况.
3、判定数列{an}的单调性考查的是an+1与an的大小关系.
〖课堂练习〗
1、数列{an}中,Sn=nn,那么a4=……………………………………………………………………( )
(A)256 (B)229 (C)27 (D)7
2、数列{an}中,an= ,如果它的前n项之和为3,那么n=………………………( )
,如果它的前n项之和为3,那么n=………………………( )
(A)16 (B)15 (C)8 (D)3
3、数列1,0,1,0,1,0,……的一个通项公式为 ;
数列1,0,-1,0,1,0,-1,0,……的一个通项公式为 ;
4、数列{an}中,a1=1, ,那么它的前4项为 .
,那么它的前4项为 .
〖能力测试〗 姓名 得分
1、数列3,7,13,21,31,…,的一个通项公式是…………………………………………………( )
(A)an=4n-1 (B)an= n2+n+1 (C)an=2+n-n2+n (D)an=n(n+1)(n-1)
2、若数列的前四项为2,0,2,0,则这个数列的通项公式不能是……………………………………( )
(A)an=1+(-1)n-1 (B)an=1-cosnp
(C)an=2sin2 (D)an=1+(-1)n-1+(n-1)(n-2)
(D)an=1+(-1)n-1+(n-1)(n-2)
3、以下通项公式中,不是2,4,8,…通项公式的是………………………………………………( )
(A)an=2n
(B)an=n2-n+2 (C)an=2n
(D)
4、已知a0=1,a1=3, ?an-1an+1=(-1)n (n∈N),则a3=……………………………………( )
?an-1an+1=(-1)n (n∈N),则a3=……………………………………( )
(A)33 (B)21 (C)17 (D)10
5、数列 中,有序数对(a,b)可以是……………………………………( )
中,有序数对(a,b)可以是……………………………………( )
(A)(21,-1) (B)(16,-1) (C)(- ,
, ) (D)(
) (D)( ,-
,- )
)
6、若数列{an}的前n项和Sn=n2-2n+3,则此数列的前三项依次是………………………………( )
(A)-1,1,3 (B)2,1,3 (C)6,1,3 (D)2,1,6
7、已知a1=1,an+1=1+ ,则a5= .
,则a5= .
8、数列{2+log2 }的第10项是
.
}的第10项是
.
9、已知数列{an}的前n项和Sn满足log2(Sn+1)=n+1,则其通项公式为 .
10、已知数列{an}的前n项和Sn,求通项公式an:
⑴Sn=5n2+3n; ⑵Sn= -2;
-2;
11、数列{an}的前n项的和为Sn=n2+pn,数列{bn}的前n项的和为 n=3n2-2n,
n=3n2-2n,
⑴如果a10=b10,求p之值
⑵取{bn}中的奇数项按照原来顺序构成数列{cn},求cn的表达式.
3.2 等差数列
〖考试要求〗
理解等差数列的概念以及推导等差数列通项公式的方法思想;掌握等差数列和公式并能加以灵活应用.
〖双基回顾〗
1、定义:
2、通项公式:
⑴
⑵
3、前n项之和 :
:
⑴
⑵
4、数a、b的等差中项:
〖知识点训练〗
1、等差数列-5,-9,-13,…,的第 项是-401;
2、已知{an}为等差数列,若a1=3,d= ,an=21,则n= ;
,an=21,则n= ;
3、已知{an}为等差数列,若a10= ,d=
,d= ,则a3= .
,则a3= .
〖典型例题〗
1、判断下列数列是否是等差数列:
⑴an =3n+5.
⑵an =3n2.
⑶数列{an}满足Sn=2n2+3n.
2、在等差数列{an}中,
⑴若a59=70,a80=112,求a101.
⑵若ap=q,aq=p (p≠q),求ap+q.
⑶若a12=23,a42=143,an=263,求n之值.
3、四个数成等差数列,它们的平方和为94,第一个数与第四个数的积比第二个数与第三个数的积少18,求此四个数.
4、等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
⑴求公差d的取值范围;
⑵指出S1、S2、S3、…、S12中哪一个最大,为什么?
5、在数列{an}中,an=11-2n.
⑴求Sn;
⑵设bn=|an|,求{bn}的前n项之和Tn.
〖课堂小结〗
1、掌握下列法则:{an}为等差数列 ;
;
2、要灵活应用等差、等比数列的通项公式(即广义通项公式);
3、三个数成等差可设它们为:a,a+d,a+2d或a-d,a,a+d;
四个数成等差(比)可设它们为:a-3d,a-d,a+d,a+3d.
〖能力测试〗
1、已知数列 是等差数列,则使
是等差数列,则使 为等差数列的数列是……………………………………(
)
为等差数列的数列是……………………………………(
)
(A) (B)
(B) (C)
(C) (D)
(D)
2、已知等差数列 中,
中, ,公差d=2,其中第一个正数项是………………………( )
,公差d=2,其中第一个正数项是………………………( )
(A)第11项 (B)第12项 (C)第13项 (D)第14项
3、在等差数列{an}中,d≠0,当n>1时,则a1an+1与a2an的大小关系是…………………………( )
(A)a1an+1>a2an (B)a1an+1<a2an (C)a1an+1=a2an (D)无法确定
4、在100和500之间能被9整除的所有数的和是…………………………………………………( )
(A)13266 (B)12699 (C)13832 (D)14500
5、设{an}是公差为-2的等差数列,若a1+a4+a7+…+a97=50,则a3+a6+a9+…+a99等于( )
(A)-78 (B)-82 (C)-148 (D)-182
6、等差数列{an}的公差d= ,且S100=145,则a1+a3+a5+…+a99等于………………………( )
,且S100=145,则a1+a3+a5+…+a99等于………………………( )
(A)52.5 (B)72.5 (C)60 (D)85
7、在等差数列{an}中,a5+a10+a15+a20=20,则S24= .
8、在两个不等正数a,b之间插入n个数,使它们与a、b组成等差数列{an},公差为d1,再插入m个数,使它们与a、b组成等差数列{bn},公差为d2,则 = .
= .
9、已知b是a、c的等差中项, 的等差中项,如果a+b+c=33,求此三数.
的等差中项,如果a+b+c=33,求此三数.
10、 一项数为偶数的等差数列,奇数项之和为24,偶数项之和为30,若最后一项比第一项大
 ,求此数列的首项、公差、及项数.
,求此数列的首项、公差、及项数.
3.3 等比数列
〖考试要求〗
理解等比数列的概念以及推导等比数列通项公式的方法思想;掌握等比数列的和公式并能加以灵活应用.
〖双基回顾〗
1、定义:
2、通项公式:
⑴
⑵
3、前n项和公式:
⑴
⑵
4、数a、b的等比中项及其条件:
〖知识点训练〗
1、在等比数列{an}中a2=2, a5=54,则q= ;
2、在等比数列{an}中a5=1, an=256,q=2,则n= .
3、公差不为0的等差数列第二、三、六项成等比数列,则公比等于 .
4、已知数列lgx+lgx2+lgx3+…+lgx10=110,求lgx+lg2x+lg3x+…+ lg10x= .
5、已知 是等比数列,且an>0,若a
是等比数列,且an>0,若a
6、方程2x2+7x+1=0的两根的等差中项为 ;等比中项为 .
〖典型例题〗
1、在等比数列{an}中,
⑴a
⑵a
*⑶q=2,a
⑷在等比数列{an}中,S4=1,S8=3,则a17+a18+a19+a20.
⑸已知等比数列{an}的公比是q= ,且a1+a3+a5+…+a99=60,求a1+a2+a3+…+a100.
,且a1+a3+a5+…+a99=60,求a1+a2+a3+…+a100.
2、已知数列{an}的前n项和满足 ,求此数列的通项公式.
,求此数列的通项公式.
3、求和:(a-1)+(a2-2)+(a3-3)+…+(an-n) .
4、已知等比数列{an}的公比q>1, 是它的前n项之和,
是它的前n项之和, 是它的前n项倒数和,并且
是它的前n项倒数和,并且 ,求满足不等式
,求满足不等式 >
> 的最小自然数.
的最小自然数.
5、正项等比数列{an}的项数为偶数,它的所有项之和等于它的偶数项和的4倍,第2、4项之积是3、4项和的9倍.⑴求a1及q;⑵问{lgan}的前几项和最大?
〖课堂练习〗在等比数列{an}中,
1、a5-a1=15,a4-a2=6,则a3= .
2、在等比数列{an}中,已知a3=1 ,S3=4
,S3=4 ,求a1、q.
,求a1、q.
〖课堂小结〗
1、{an}为等比数列 2、要灵活应用等比数列的广义通项公式.
2、要灵活应用等比数列的广义通项公式.
3、三个数成等比可设它们为:a,aq,aq2或a/q,a,aq;
四个数成等比可设它们为: a/q3,a/q,aq,aq3;
4、运用等比数列和公式时,一定得注意q的取值.
〖能力测试〗
1、若a、b、c成等比数列,则函数y=ax2+bx+c的图象与x轴交点的个数是…………………( )
(A)0个 (B)1个 (C)2个 (D)0个或2个
2、下列四个命题:
①公比q>1的等比数列的各项都大于1;②公比q<0的等比数列是递减数列;③常数列是公比为1的等比数列; ④{lg2n}是等差数列而不是等比数列
正确的个数是……………………………………………………………………………………( )
(A)0 (B)1 (C)2 (D)3
3、数列{an}的前n项之和为Sn=an-1,那么此数列是……………………………………………( )
(A)等比数列 (B)等差数列 (C)等比或等差数列 (D)等比不是等差数列
4、已知数列{an}的通项公式为an=22n-1,则该数列的前5项的和为……………………………( )
(A)62
(B) (C)
(C) (D)682
(D)682
5、一个数列{ an }是递增的等比数列,公比是q,则该数列的……………………………………( )
(A)q>1 (B)a1>0,q>1
(C)a1<0,q<1 (D)a1>0,q>1或a1<0,0<q<1
6、一个数列{an}中,a1=15,a45=90,如是等差数列,则a60= ;如是等比数列,则a60= .
7、等比数列 中,an+2=an,则实数公比q= 、an+3=an,则实数公比q= .
中,an+2=an,则实数公比q= 、an+3=an,则实数公比q= .
8、三数成等差数列,它们的和等于15,如果它们分别加上1,3,9就成为等比数列,求这三个数.
9、在3和2187之间插入若干个正数,使所有数组成等比数列,且插入的这些正数之和为1089,求插入的这些正数各是多少?
10、如果一个三角形的三边成等比数列,求公比q的取值范围.
3.4 等差等比数列综合应用
〖考试要求〗
掌握运用等差(比)数列中的常用思想方法(定义法、递推法、倒序相加法、错位相减法等).
〖课前预习〗
1、下列说法正确的是…………………………………………………………………………………( )
(A)数列 中,若
中,若 ,(q为常数,n∈N),则
,(q为常数,n∈N),则 是等比数列
是等比数列
(B)等比数列 中,若m,n,p成等差数列,且m,n,p∈N则
中,若m,n,p成等差数列,且m,n,p∈N则
(C)lg2,lgm,lg8是成等差数列,则2,m,8成等比数列且m=±4
(D) 是a,b,c成等比数列的充要条件
是a,b,c成等比数列的充要条件
2、数列 的前项n和
的前项n和 则
则 的值为……………………………………………( )
的值为……………………………………………( )
(A)1100 (B)112 (C)988 (D)114
3、等差数列共有2n+1项,所有奇数项的和为132,所有偶数项的和为120,则n=………………( )
(A)9 (B)10 (C)11 (D)不确定
4、数列{an}的前n项和Sn=2n2+n-1,则它的通项公式是…………………………………………( )
(A)an=4n-1 (B)an=4n-2 (C)
 (D)
(D)

5、在等差数列{an}中,已知a3:a5=3:4,则S9:S5的值是…………………………………………( )
(A)27:20 (B)9:4 (C)3:4 (D)12:5
6、在等比数列{ an }中,an =2´3 n-1,则该数列中前n个偶数项的和等于…………………………( )
(A)3 n-1 (B)3(3 n-1) (C) (9 n-1) (D)
(9 n-1) (D) (9 n-1)
(9 n-1)
7、若 ,
, ,
, 成等差数列,则x的值为 .
成等差数列,则x的值为 .
8、 .
.
〖典型例题〗
1、一个数列{an}中,当n为奇数时,an=5n+1,当n是偶数时,an= ,求此数列的前2n项之和.
,求此数列的前2n项之和.
2、方程 =0的四个根组成一个首项为
=0的四个根组成一个首项为 的等差数列,则|m-n|=…( )
的等差数列,则|m-n|=…( )
(A)1
(B) (C)
(C)  (D)
(D)
3、数列{an}满足: ,并且a1≠a2.⑴求实数p之值;⑵求证{an}是A.P
,并且a1≠a2.⑴求实数p之值;⑵求证{an}是A.P
4、已知数列 是等差数列,
是等差数列,
⑴求证:数列 也是等差数列;
也是等差数列;
⑵若 ,求这两个数列
,求这两个数列 、
、 的通项公式.
的通项公式.
5、设{an}是等差数列,bn= ,已知b1+b2+b3=
,已知b1+b2+b3= ,b1b2b3=
,b1b2b3= ,
,
⑴求证:数列{bn}是等比数列; ⑵求等差数列{an}的通项an.
6、若两个等差数列{an}与{bn}的前n项和之比为Sn:S¢n=(4n+1):(9n+3),求a20:b20.
7、数列{an}、{bn}分别是等比数列、等差数列,满足ai>0,bj>0,b2-b1>0,是否存在常数k,使: 是常数?
是常数?
〖能力测试〗
1、若{an}是等比数列,其公比是q,且-a5,a4,a6成等差数列,则q等于……………………( )
(A)1或2 (B)1或-2 (C)-1或2 (D)-1或-2
2、若等差数列{an}单调递增,且a3+a6+a9=12,a
(A)n-2 (B)-n+16 (C)n-2 或-n+16 (D)n-2
3、等比数列{an}中,已知对任意正整数n,a1+a2+…+an=2n-1,则 等于( )
等于( )
(A)(2n-1)2
(B) (2n-1) (C)4n-1
(D)
(2n-1) (C)4n-1
(D) (4n-1)
(4n-1)
4、已知数列 的通项为
的通项为 若要使此数列的前n项和最大,则n的值为…………( )
若要使此数列的前n项和最大,则n的值为…………( )
(A)12 (B)13 (C)12或13 (D)14
5、已知数列1,1,2,…,它的每一项由一个等比数列和一个首项为0的等差数列对应项相加而得到,那么这个数列的前10项的和为………………………………………………………………( )
(A)467 (B)557 (C)978 (D)1068
6、正数a、b的乘积ab是a4+a2b2与b4+a2b2的一个等比中项,则ab的…………………………( )
(A)最大值为 (B)最小值为
(B)最小值为 (C))最大值为
(C))最大值为 (D)最小值为
(D)最小值为
7、在等差数列{an}中,如果a6+a9+a12+a15=20,则S20= .
8、已知数列{an}是等比数列,首项a1=8,令bn=log2an,若数列{bn}的前7项的和S7最大,且S7≠S8,求数列{an}的公比q的取值范围.
*9.已知函数

*10、一个公差不为零的等差数列{an}共有100项,首项为5,其第1、4、16项分别为正项等比数列{bn}的第1、3、5项.
⑴求{an}的各项的和S;
⑵若{bn}的末项不大于 ,求{bn}项数的最大值N;
,求{bn}项数的最大值N;
⑶记{an}前项和为Sn,{bn}前项和为Tn,问是否存在自然数m,使Sm=TN?
3.5 特殊数列求和
〖考试要求〗
掌握等差数列与等比数列前n项和公式,并能够应用这些知识解决一些简单的问题.
〖学习指导〗
1、掌握倒序求和法与错位相减法。
2、记住一些常见结论并且会应用之,学会分析通项的结构并且对通项进行分拆。
〖知识点训练〗
1、记住下列结论:
⑴1+2+3+…+n= ;⑵1+3+5+…+(2n-1)= ;
2、求和:
⑴ =
.
=
.
⑵ = .
= .
〖典型例题〗
1、求和:S=1-2+3-4+…+ n.
n.
2、求和:S=1+
*3、
4、求和:
4、⑴求数列:1,1+2,1+2+3,…,1+2+3+…+n,…的前n项之和
*⑵求数列:1,2+3,4+5+6,7+8+9+10,…的通项公式及前n项之和
5、如果0<n<100并且n∈N,求S= 的最小值.
的最小值.
〖课堂练习〗
1、求和:
*2、求分母为3,包含在整数m与n之间的所有不可约的分数之和.
〖能力测试〗
1、数列:1,1+2,1+2+22,1+2+22+23,…的前n项之和为…………………………………( )
(A)2n-1 (B)2n+1-n-2 (C)2n+1-n (D)2n+1-1
2、数列{an}中,an= (-1)n-1(4n-3),那么它的前100项之和为……………………………………( )
(A)200 (B)-200 (C)400 (D)-400
3、数列{an}中,前n项之和Sn=1-5+9-13+17-21+…+(-1)n-1(4n-3),则S15+S22-S31= .
4、如果数列{an}的前n项之和为Sn=3+2n,那么 =
.
=
.
5、如果数列{an}中,an= ,求前n项之和Sn.
,求前n项之和Sn.
6、如果an=12+22+…+n2,求数列 的前n项之和.
的前n项之和.
7、函数
⑴求
⑵设a1=1,an=- ,求数列{an}的通项公式
,求数列{an}的通项公式
⑶求和S= .
.
3.6 等差等比数列应用题
〖考试要求〗
能运用等差(比)数列知识解决相关的实际应用问题..
〖学习指导〗
1、等差数列应用题一般是解决增加或减少相同数量的问题;等比数列应用题一般是解决增加或减少相同百分率的问题,转化为数学问题之后,运算量偏大,所列的方程不是高次方程就是指对数方程,有时还要涉及到对数、近似计算(二项式定理)的问题。解决实际问题的关键是闯过阅读理解这一关。
2、请阅读课本第一册(上)P124―125,P133―136,了解关于银行存款计算.
〖典型例题〗
1、用分期付款的方式购买价格为1150元的冰箱,如果购买时先付150元,余款分20次付完。以后每月付50元加上欠款的利息。如果月利息为1%,那么第10个月要付多少钱,总共要付多少钱?
2、某林场的树木以每年25%的增长率生长,计划从今年起每年冬季砍伐相同数量的木材,并且还要实现20年后木材储量翻两番.问每年的砍伐量应为现在木材总量的多少?(lg2=0.3)
3、某渔业公司今年初用98万元购进一艘鱼船用于捕捞,第一年需要各种费用12万元,从第二年起包括维修费在内每年所需费用比上一年增加4万元,该船每年捕捞总收入50万元.
(Ⅰ)该船捕捞几年开始盈利?
(Ⅱ)该船捕捞若干年后,处理方案有两种,问哪一种方案合算?为什么?
⑴当年平均利润最大时以26万元的价格卖出;
⑵当盈利总额达到最大时以8万元价格卖出;
4、某县有土地1万亩,其中有70%的沙漠,从今年起进行绿化改造,每年把原有沙漠的16%改造为绿地,同时原有绿地的4%又被变为沙漠,设从今年起第n年有绿地an万亩.
⑴求数列{an}的通项公式;
⑵至少经过几年,绿化面积可以超过60%
*5、某工厂A车间现有职工30人,平均每年可创产值a万元(a为正常数),为了适应市场经济的发展需要,计划对A车间人员进行裁减.据评估,在生产条件不变的情况下,裁减1人时,留岗职工平均每人每年创造产值增加5%;在一定范围内,裁减n+1个人时比裁减n人时,留岗职工平均每人每年创造产值增加5%(n∈N*),为使全年创造的总产值最大,A车间应裁员多少人?
〖能力测试〗
1、某产品成本不断下降,若每隔三年价格要降低25%,现在价格是640元,则12年后的价格是( )
(A)270元
一、选择题(60分)
1、已知数列{an}的前n项之和Sn=2n2-3n+1,那么a4+a5+…+a10=………………………( )
(A)139 (B)171 (C)150 (D)161
2、等差数列{an}中,已知d=-2,a1+a4+…+a31=50,那么a2+a5+…+a32=………………( )
(A)27 (B)28 (C)-27 (D)-28
3、在等比数列{an}中,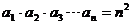 ,则a3+a5=……………………………………(
)
,则a3+a5=……………………………………(
)
(A)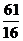 (B)
(B)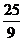 (C)
(C)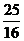 (D)
(D)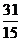
4、已知数列{an}是等比数列n∈N*,那么下列结论正确的是…………………………………( )
(A)an?an+1>0 (B)an?an+2>0
(C)an?an+1?an+4>0 (D)an?an+2?an+4>0
5、已知6,a,b,48成等差数列,6,c,d,48成等比数列,那么a+b+c+d=……………( )
(A)60 (B)70 (C)80 (D)90
6、等差数列{an}中,a1+a4+a7=15,a3+a6+a9=3,那么S9=……………………………………( )
(A)18 (B)27 (C)36 (D)45
7、等差数列{an}中,an<0,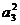 +
+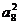 +
+
(A)-9 (B)-11 (C)-13 (D)-15
8、等差数列中,a30=50,a50=30,那么a80=………………………………………………………( )
(A)0 (B)80 (C)-20 (D)20
9、如果数列{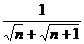 }的前n项之和为10,那么n=……………………………………( )
}的前n项之和为10,那么n=……………………………………( )
(A)11 (B)99 (C)120 (D)121
10、在等比数列{an}中,Sn=3n-1,那么a12+a22+…+an2=……………………………………( )
(A)9n-1 (B)3n-1
(C)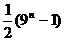 (D)
(D)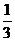 (3n-1)
(3n-1)
11、等差数列中,S13=39,那么a7=………………………………………………………………( )
(A)3 (B)6 (C)9 (D)12
12、等差数列{an}的第一、二、五项依次成等比数列,则此等差数列的公差为首项的…………( )
(A)3倍 (B)2倍 (C)-2倍 (D)2或者0倍
二、填空题(16分)
13、等差数列{an}中,前n项之和为Sn=2n2-13n,那么当Sn最小时, n= .
14、x、y是正数,x,a,b,y成等差,x,m,n,y成等比,则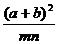 的取值范围是
.
的取值范围是
.
15、在等比数列{bn}中,S4=4,S8=20,那么S12= .
16、现有200根相同的钢管,要求把它们堆放成正三角形垛并且使得剩余的钢管尽可能的少,那么剩余钢管的根数= .
三、解答题(74分)
17、如果数列{an}的前n项之和为Sn=-n2+3n-4,求其通项公式.
18、在等比数列{an}中,a3=3,S3=9,求其公比.
19、有四个实数,前3个成等比数列,它们的积为216,后3个数成等差数列,它们的和为12,求此四数.
20、已知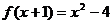 ,等差数列{
,等差数列{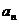 }中,
}中,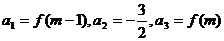 .
.
⑴求实数m;
⑵求此数列的通项公式;
⑶求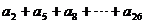 之值.
之值.
21、一种化工产品的单价随纯度的提高而提高。某化学公司计划要用单价为A元/千克的原料100千克进行提纯,每次提纯后产品的总价值按照如下方法计算:每提纯一次,产品的重量减少2%,单价是提纯前的1.3倍,在此基础上每提纯一次,需要扣除加工费是本次提纯前总价值的7.4%.
⑴问第一次提纯后的总价值为多少元?
⑵求使此产品总价值翻一番的最小提纯次数n(参考数据:lg2=0.3010,lg3=0.4771)
22、是否存在一个实数等比数列{an},同时满足:
⑴a3、a4是方程x2-4x+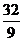 =0的根;
=0的根;
⑵至少存在一个自然数m,使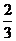
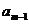 ,
,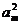 ,
,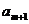 +
+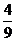 成等差数列?
成等差数列?
如果存在,求出通项公式,如果不存在,说明理由!