平遥县2009年4月高三高补质检
数学试题(文科)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。 命题人:邓国进 张建平
第Ⅰ卷( 选择题 共60分 )
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一项是符合要求的)
1.已知函数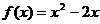 ,则“
,则“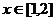 ”是“
”是“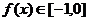 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.含有3个元素的集合既可表示为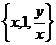 ,又可表示为
,又可表示为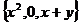 ,则x2009+y2009的值是( )
,则x2009+y2009的值是( )
A.1
B.―
3.已知函数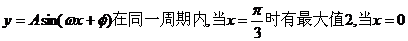 时有最小值―2,那么函数的解析式为 ( )
时有最小值―2,那么函数的解析式为 ( )
A.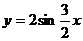 B.
B.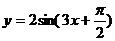
C.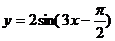 D.
D.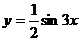
4.某校有学生4500人,其中高三学生1500人.为了解学生的身体素质情况,采用按年级
分层抽样的方法,从该校学生中抽取一个300人的样本.则样本中高三学生的人数为( )
A 150
B
5.函数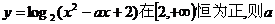 的取值范围是 ( )
的取值范围是 ( )
A. B.
B.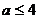
C.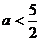 D.
D.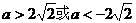
6.设 的范围是( )
的范围是( )
A.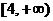 B.
B.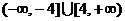 C.
C.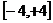 D.
D.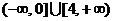
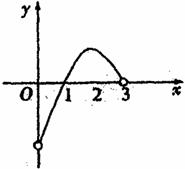
7.已知 的图像如图所示,那么不等式
的图像如图所示,那么不等式 的解集是 ( )
的解集是 ( )
|
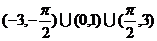

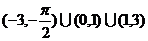
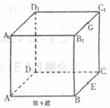 8.如图,正方体ABCD―A1B
8.如图,正方体ABCD―A1B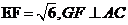 的点F有( )
的点F有( )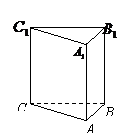 C. 2个
D.无数个
C. 2个
D.无数个 9.某人有4种颜色的灯泡(每种颜色的灯泡足够多),
9.某人有4种颜色的灯泡(每种颜色的灯泡足够多),
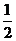 B.最小值
B.最小值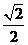 D.最小值
D.最小值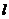 ∩BD1=P,交正方体表面于M、N两点,
∩BD1=P,交正方体表面于M、N两点,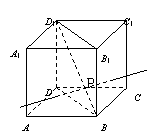 且M、N在底面的射影分别为M1、N1,直线
且M、N在底面的射影分别为M1、N1,直线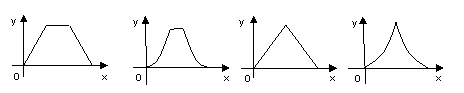
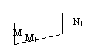
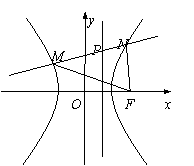
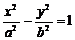 的左右两支分别交于M、N两点,与双曲线的右准线交于P点,F为右焦点,若|FM| = 2|FN|,
的左右两支分别交于M、N两点,与双曲线的右准线交于P点,F为右焦点,若|FM| = 2|FN|,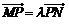 ,则实数
,则实数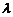 的取值为( )
的取值为( ) 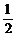 B.
B.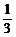
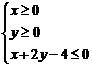 恰好被面积最小的圆
恰好被面积最小的圆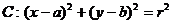 及其内部所覆盖.则圆
及其内部所覆盖.则圆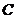 的方程为
。
的方程为
。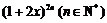 展开式中含x奇次幂的系数和
展开式中含x奇次幂的系数和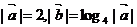 且
且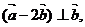 ,则向量
,则向量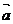 与向量
与向量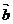 的夹角是_________。
的夹角是_________。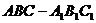 中,D为棱
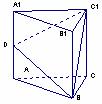
中,D为棱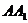 的中点,若截面
的中点,若截面 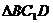 是面积为6的直角三角形,则此三棱柱的体积为
。
是面积为6的直角三角形,则此三棱柱的体积为
。
 三、解答题:(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
三、解答题:(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)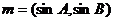 ,
, ,
,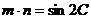 ,且A、B、C分别为
,且A、B、C分别为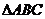 的三边所对的角。
的三边所对的角。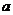 、
、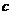 、
、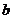 成等差数列,且
成等差数列,且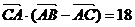 ,求边
,求边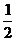 ,乙投篮命中的概率为
,乙投篮命中的概率为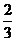 .
.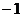 分,求乙所得分数至少8分的概率.
分,求乙所得分数至少8分的概率.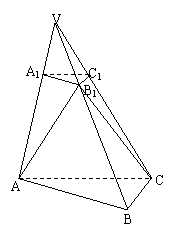 如图,己知平面A1B
如图,己知平面A1B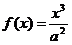 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为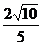 ,函数
,函数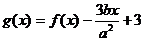 .
.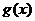 在
在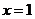 处有极值,求
处有极值,求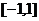 上为增函数,且
上为增函数,且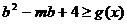 在区间
在区间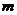 的取值范围.
的取值范围.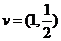 为方向向量的直线
为方向向量的直线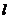 过点
过点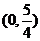 ,抛物线
,抛物线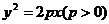 的顶点关于直线
的顶点关于直线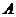 、
、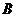 是抛物线
是抛物线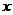 轴的直线
轴的直线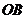 与直线
与直线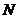 ,若
,若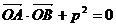 (
(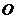 为坐标原点,
为坐标原点,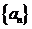 中,
中,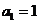 ,
,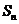 为其前n项和,等比数列
为其前n项和,等比数列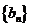 的公比q满足
的公比q满足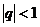 ,
,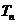 为其前n项和,若
为其前n项和,若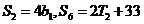 又
又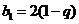
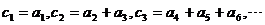 ,求
,求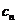 的表达式;
的表达式; 14,
14,
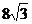
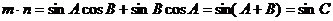 ,………3分
,………3分
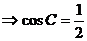 ,又
,又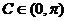 ,∴
,∴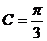 ………………………5分
………………………5分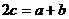 ,又∵
,又∵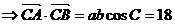
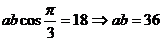 ,………………………………………………7分
,………………………………………………7分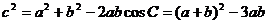

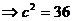 ,∴
,∴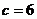 ………………………………………………10分
………………………………………………10分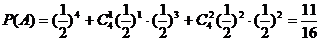 ……………………………2分
……………………………2分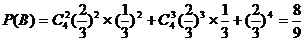 …………………………… 4分
…………………………… 4分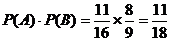 ……………………………6分
……………………………6分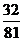 +
+ 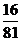 =
=
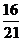 ……………………12分
……………………12分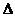 AB
AB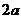 ,则AH=
,则AH=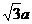 为A到平面VBC的距离。……..8分
为A到平面VBC的距离。……..8分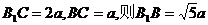 又Rt
又Rt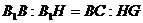
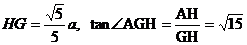
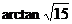 ……………………...12分
……………………...12分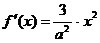 ,∴由
,∴由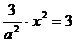 有
有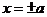 ,即切点坐标为
,即切点坐标为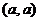 ,
,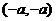
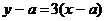 ,或
,或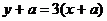 ……………………2分
……………………2分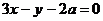 或
或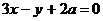
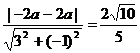 ,解得
,解得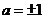 ,∴
,∴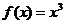 ,
,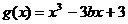 ……………………5分
……………………5分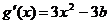 ,
,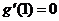 ,
,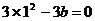 ,解得
,解得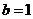 ,∴
,∴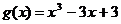 ……………………8分
……………………8分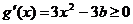 在区间
在区间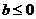 ,又∵
,又∵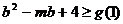 ,
,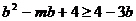 ,∴
,∴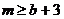 在
在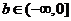 上恒成立,∴
上恒成立,∴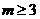
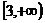 …………12分
…………12分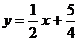 ①
①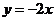 ②
②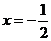
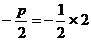 ,
,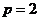 ∴抛物线
∴抛物线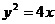 ……………………………6 分
……………………………6 分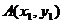 ,
,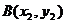 ,
,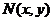 ,由
,由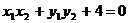
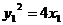 ,
,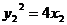 ,解得
,解得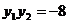 ③
③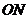 :
: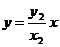 ,即
,即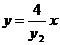 ④
④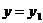 ,得点
,得点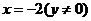 ……………………………12分
……………………………12分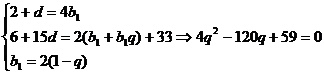
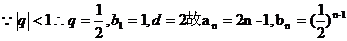 ……..6分
……..6分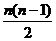 个项
个项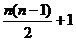 项为
项为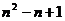 ,故{Cn}是首项为
,故{Cn}是首项为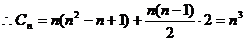 ……..12分
……..12分