高一数学第一次月考
数学试题
出题人:鲍军峰、徐伟 审题人:任佩文
第I卷
一、选择题 (每小题5分,共60分)
1、设集合M={(1,2)},则下列关系成立的是 ( )
A.
2、下列语句中,不能成为命题的是 ( )
 A.
A. 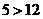 B.
B. 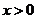 C.
C. 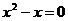 的根是1 D.
的根是1 D. 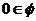
3、如图 I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是( )
A.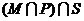 B.
B. 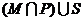
C. 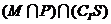 D.
D. 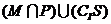
4、 如果集合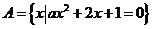 中只有一个元素,则a的值是 ( )
中只有一个元素,则a的值是 ( )
A.0
B.0
或
5、全集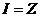 ,集合
,集合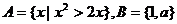 ,若
,若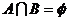 ,这样的集合B ( )
,这样的集合B ( )
A、不存在 B、有1个 C、有两个 D、有三个
6、不等式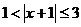 的解集为 ( )
的解集为 ( )
A.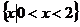 B.
B.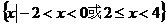
C.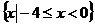 D.
D.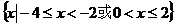
7、设集合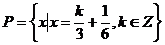 ,
,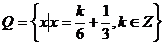 ,则( )
,则( )
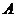 .
. 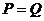
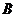 .
. 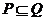
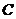 .
. 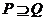
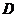 .
. 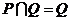
8、下列命题错误的有 ( )
① 很小的实数可以构成集合;
②
集合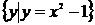 与集合
与集合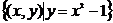 是同一个集合;
是同一个集合;
③ 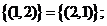
④ 集合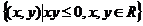 是指第二、四象限内的点集。
是指第二、四象限内的点集。
A.0个 B.1个 C.3个 D.4个
9、设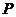 和
和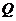 是两个非空集合,定义
是两个非空集合,定义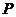 与
与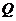 的差集为
的差集为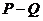 =
=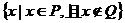 , 则
, 则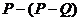 等于 ( )
等于 ( )
A.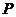 B.
B. 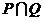 C.
C. 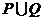 D.
D. 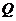
10、已知集合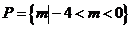 ,
,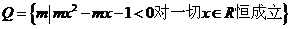 ,那么下列关系中成立的是 ( )
,那么下列关系中成立的是 ( )
A.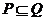 B.
B. 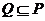 C.
C. 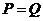 D.
D. 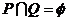
11、命题“对任意的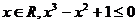 ”的否定是 ( )
”的否定是 ( )
A.不存在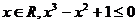 B.存在
B.存在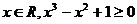
C.存在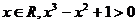 D. 对任意的
D. 对任意的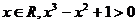
12、设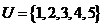 ,若
,若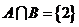 ,
,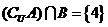 ,
,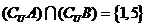 ,则下列结论正确的是
( )
,则下列结论正确的是
( )
A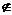 A且3
A且3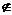 B B.3
B B.3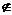 B且3
B且3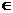 A C.3
A C.3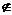 A且3
A且3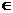 B D.3
B D.3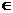 A且3
A且3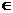 B
B
第II卷
二、填空题(每小题5分,共20分)
13、 集合M={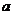 |
| 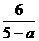
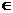 N,且
N,且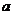
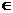 Z},用列举法表示集合M=
Z},用列举法表示集合M=
14、已知集合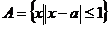 ,
,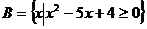 ,若
,若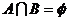 ,则实数
,则实数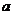 的取值范围是
.
的取值范围是
.
15.已知不等式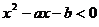 的解集为
的解集为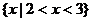 ,不等式
,不等式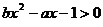 的解集是
.
的解集是
.
16、集合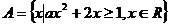 ,若集合A中只有一个元素,则
,若集合A中只有一个元素,则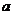 的值为
.
的值为
.
三、解答题(本大题共8小题,共70分)
17、(本小题10分)
用描述法表示下列集合
(1)不等式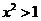 的解集;
的解集;
 (2)函数
(2)函数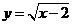 的自变量
的自变量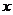 的集合
的集合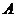 与函数值
与函数值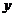 的集合
的集合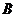 ;
;
(3)如图阴影部分的点的集合 (含边界)。
18、(本小题10分)
设全集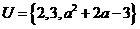 ,
,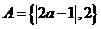 ,
,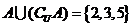 ,求实数
,求实数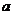 的值。19、(本小题9分)解不等式
的值。19、(本小题9分)解不等式 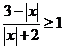 .
.
20、(本小题9分)
设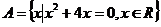 ,
,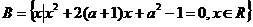 若
若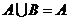 ,求实数
,求实数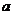 的取值范围。
的取值范围。
21、(本小题8分)
已知命题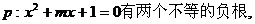
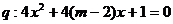 无实根,若
无实根,若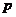 或
或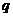 为真命题,
为真命题,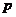 且
且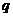 为假命题,求实数
为假命题,求实数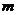 的取值范围。
的取值范围。
22、(本小题8分)解关于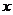 的不等式:
的不等式: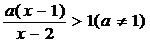 。
。
23、(本小题8分)已知集合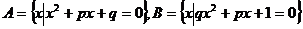 同时满足
同时满足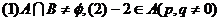 ,求
,求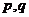 的值。
的值。
24、(本小题8分)已知二次函数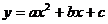 ,且不等式
,且不等式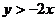 的解集为
的解集为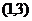 。
。
(1)若方程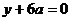 有两个相等的根,求二次函数的表达式。
有两个相等的根,求二次函数的表达式。
(2)若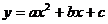 的最大值为正数,求
的最大值为正数,求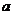 的取值范围。
的取值范围。
数学答案
1C 2B 3C 4B 5C 6D 7B 8D 9B 10A 11C 12B
二、填空题
13、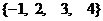 14、
14、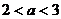
15、{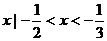 }
16、
}
16、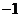
三、解答题
17、解:(1)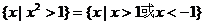
(2)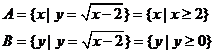
(3)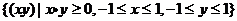
18、解:由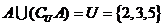
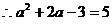
得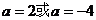
经检验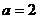 符合条件
符合条件
而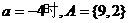
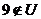 故不成立,
故不成立,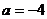 舍去,
舍去,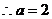
19、解不等式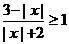
解: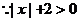
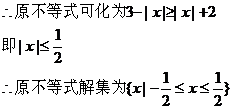
20、解: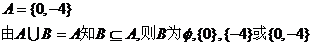
(1)若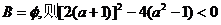
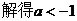
(2)若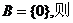
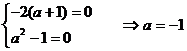
(3)若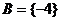 ,则
,则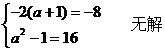
(4)若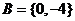 ,则
,则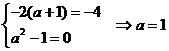
综上,实数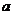 的取值范围是
的取值范围是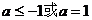 。
。
21.解:若P为真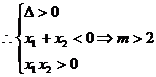
若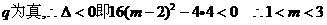
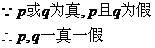
若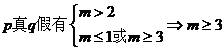
若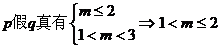
综上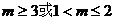
22.
解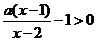
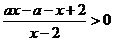
可变形为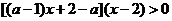
相应方程的根为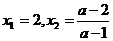
若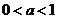 时
时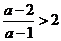 ,
,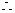 不等式的解集为
不等式的解集为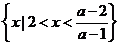
若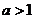 时
时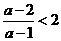 ,
,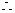 不等式的解集为
不等式的解集为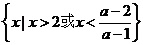
若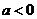 时
时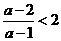 ,
,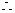 不等式的解集为
不等式的解集为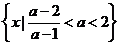
若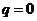 时
时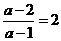 ,
,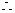 不等式的解集为
不等式的解集为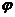
23.
解: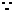
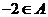
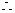
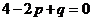 即
即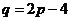
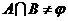
 方程组
方程组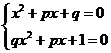 有解
有解
即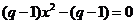 有解
有解
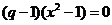
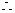 当
当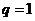 时成立,此时
时成立,此时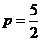
当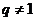 时,
时,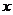 可能值为
可能值为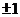
即A中必有另一元素1或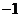
若A中有元素1代入有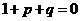 ①
①
①与 联立得
联立得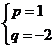
若A中有元素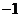 代入有
代入有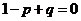 ②
②
②与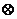 联立得
联立得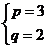
综上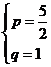 或
或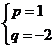 或
或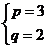
24.解: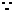
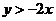
整理得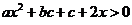
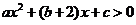
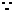 解集为
解集为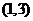
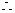
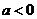 ,且
,且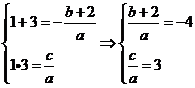 ①
①
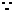
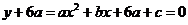 有两相等实根
有两相等实根
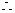
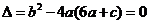 ②
②
①②联立得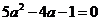 ,
,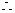
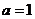 或
或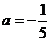
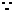
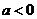 ,
,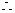
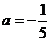
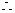
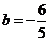 ,
,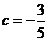
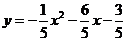
(2)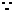 函数开口向下
函数开口向下
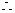 最大值为
最大值为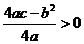
由①得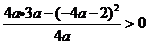
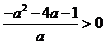
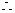
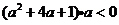
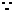
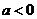
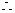
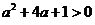
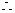
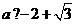 或
或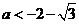
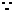
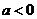
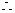
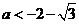 或
或