2009-2010学年度辽宁省营口市七中初三11月月考
数学试卷
一.选择题(每小题3分,共24分)
1.与下边二视图所对应的直观图是( )






2.一架
A.5sin40° B.5cos40° C. D.
D.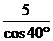
3.根据下列表格的对应值:
3.23
3.24
3.25
7.26
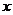 2+
2+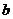
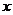 +
+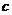
0.06
0.02
0.03
0.07
判断方程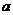
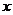 2+
2+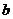
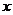 +
+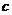 =0(
=0(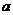 ≠0.
≠0.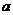 ,
,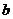 ,
,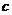 常数)的一个解
常数)的一个解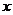 的范围是( )
的范围是( )
A.3<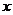 <3.23 B.3.23<
<3.23 B.3.23<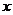 <
<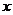 <3.25 D.3.25<
<3.25 D.3.25<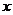 <3.26
<3.26
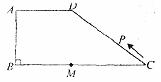
4.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发观身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身商是1.5m两个路灯的亮度都是9m.则两路灯之间的距离是( )
A.24 m B.25m C.28m D.30 m
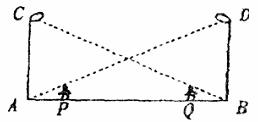
5.方程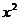 -9
-9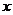 +18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A.12 B.12或15 C.15 D.不能确定
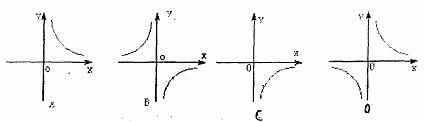
6.在下图中,反比例函数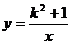 的图象大致是 ( )
的图象大致是 ( )
7.如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于 E,若CE=3,则BE的长是( )
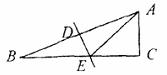
A.3 B.6 C.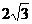 D.
D. 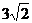
8.将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,出现的数字分别为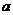 、
、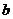 、
、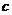 ,则
,则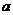 、
、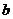 、
、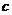 是直角三角形三边长的概率是( )
是直角三角形三边长的概率是( )
A.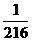 B.
B.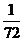 C.
C.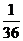 D.
D.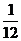
二.填空题(每小题3分,共24分)
9.已知菱形的一个内角为60°,一条对角线的长为2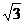 ,则另一条对角线的长为_______.
,则另一条对角线的长为_______.
10.用配方法解方程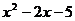 =0时,原方程应变形为______________。
=0时,原方程应变形为______________。
11.如图所示,在梯形ABCD中.AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8。动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有_______个.
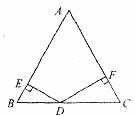
12.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB 于点E,DF⊥AC于点F.若BC=2,则DE+DF=_______
13.已知函数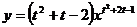 ,当
,当 =_______时,此函数是二次函数,当
=_______时,此函数是二次函数,当 =_______时,此函数是反比例函数
=_______时,此函数是反比例函数
14.在一个暗箱里放有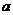 个除颜色外其它完全相同的球,这
个除颜色外其它完全相同的球,这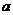 个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量反复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出
个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量反复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出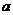 大约是______
大约是______
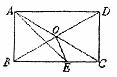
15.如图,在矩形ABCD中,AC、BD相交于D,AE平分∠BAD,交BC于E,若∠CAE=15°,则∠BOE的度数为_______
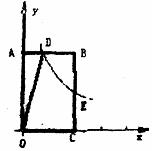
16.如图,双曲线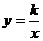 (
(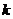 >0)经过矩形OABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3。则双曲线的解析式为______________
>0)经过矩形OABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3。则双曲线的解析式为______________
三.解答题
17.三根垂直于地面的木杆甲、乙、丙,在路灯下乙、丙的影于如图 所示,试确定路灯灯泡的位置,再作出甲的影子(不写作法,保留作图痕迹)。

18.如图,有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的图形,小明将这四张纸牌背面朝上洗匀后随机摸出一张,放回后洗匀再随机摸出一张。
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌A,B,C,D表示)
(2)求两次摸牌的牌面图形既是中心对称图形又是轴对称图形的概率。

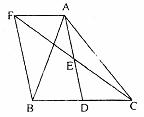
19.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF。
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论。
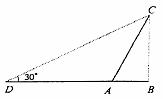
20.如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为 =1:0.5求山的高度(不计测角仪的高度,结果保留根号)。
=1:0.5求山的高度(不计测角仪的高度,结果保留根号)。
21.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满。当每个房间每天的定价每增加10元时,就会有一个房间空闲,对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间每天的定价增加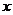 元,求:
元,求:
(1)房间每天的入住量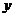 (间)关于
(间)关于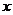 (元)的函数关系式;
(元)的函数关系式;
(2)当每个房间的定价为每天多少元时,该宾馆客房部每天的利润达到15210元?
22.(1)求证:关于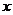 的一元二次方程
的一元二次方程 =0不论
=0不论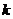 取何值,方程都有两个不相等的实数根。
取何值,方程都有两个不相等的实数根。
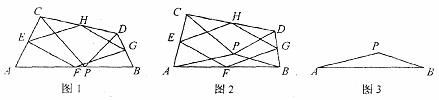
(2)若△ABC的两边AB,AC的长是关于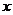 的方程
的方程 =0的两根,
=0的两根,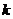 为何值时,△ABC是以BC为斜边的直角三角形:
为何值时,△ABC是以BC为斜边的直角三角形:
四.解答题(12分,)
23.如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD。使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答。不必说明理由:
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由:
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
五.解答题(14分)
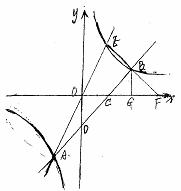
24.如图,直线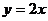 与双曲线
与双曲线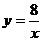 交于点A、E,直线AB交双曲线于另一点B,与
交于点A、E,直线AB交双曲线于另一点B,与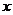 轴、
轴、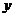 轴分别交丁C、D,过B点作BG⊥
轴分别交丁C、D,过B点作BG⊥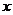 轴于G点,且BG/OG=1/2,直线EB交
轴于G点,且BG/OG=1/2,直线EB交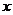 轴于点F。
轴于点F。
(1)求A、B两点的坐标.
(2)求∠OFE的正切值
(3)求证:△COD∽△CBF。