2009-2010学年江苏省盐城初级中学第一学期八年级期末考试
数学试卷
一、精心选一选(本大题共有8小题,每小题3分,共24分. 注意每小题所给出的四个选项中,只有一项是正确的. 请把正确选项前的字母代号填在题后的括号内. 相信你一定会选对!)
1、下列4个图案中,既是轴对称图形又是中心对称图形的有( )

A.1个 B.2个 C.3个 D.4个
B.2个 C.3个 D.4个
2、给出下列长度的四组线段:①1,2,2;②5,13,12;③6,7,8;④3,4,5.
其中能组成直角三角形的有( )
A.①② B.②③ C.②④ D.③④
3、八年级(1)班的10名同学的期末体育测试成绩如下: 80,86,86,86,86,87,
88,89,89,95,这些成绩的众数是( )
A.85 B.
4、若点P关于x轴的对称点的坐标是(2,3),则点P关于原点的对称点的坐标是( )
A.(-3,-2) B.(2,-3) C.(-2,-3) D.(-2,3)
5、已知等腰三角形的两边长分别为
A.
6、下列判断错误的是( )
A.对角线互相垂直的平行四边形是正方形
B.四个角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.一组对边平行且一组对角相等的四边形是平行四边形
7、直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
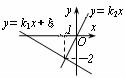
A.x>-1 B.x<-
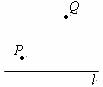
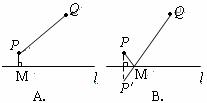
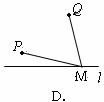
8、如图,直线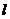 是一条河,P、Q两地相距
是一条河,P、Q两地相距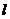 的距离分别为
的距离分别为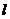 上的某点M处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )
上的某点M处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )
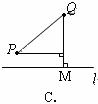
二、细心填一填(本大题共有10小题,每小题3分,共30分.相信你一定会填对的!)
9、25的平方根为 ;9的算术平方根是 ; 的立方根为-2.
10、2010年“元旦”期间无锡市旅游人数达136 000人次,数据“136
11、已知点P1(a,3)与P2(-2,b)关于y轴对称,则ab的值为 .
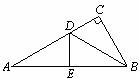
12、如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=30°,则∠CBD=
°.
13、在某校艺术节舞蹈比赛中,六名评委对八(1)班舞蹈队打分如下:7.5分,8.3分,7.7分,9.2分,8.1分, 7.9分,去掉一个最高分和一个最低分后的平均分是___________分
14、一次函数y=-2x+6与x轴的交点坐标是________,与y轴的交点坐标是________,与坐标轴围成的三角形的面积为 .
15、直角三角形三边长分别为3,4,m,则m= .
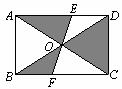
16、如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
17、在△ABC中,∠A=50°,当∠B的度数= 时,△ABC是等腰三角形.
18、如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=

三、认真答一答(本大题共6小题,共54分. 只要你积极思考, 仔细运算, 一定会解答正确的!)
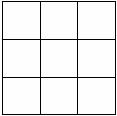
19、(本小题满分8分)如图,正方形网格中的每个小正方形边长都是1.(利用网格线进行画图)
⑴在图1中画出以格点为顶点、面积为5的正方形;
⑵在图2中已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;
⑶在图3中①画出一个以格点为端点直角边长为2、3的直角△ABC(∠C=90°);
②在AB上找一点D,使得D到CB、CA的距离相等;
③在射线CD上找一点E到三角形某两点的距离相等.
 图一
图一
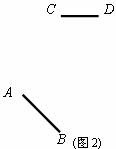
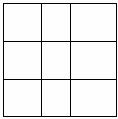 图3
图3
(友情提醒:别忘了标上字母噢!)
20、(本小题满分8分)一家公司对A、B、C三名应聘者进行了创新、综合知识和语言三项素质测试,他们的成绩如下表所示:
测试项目
测试成绩
A
B
C
创新
72
85
67
综合知识
50
74
70
语言
88
45
67
(1)如果根据三项测试的平均成绩确定录用人选,你选谁?请说明理由;
(2)根据实际需要,广告公司给出了选人标准:将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人的测试成绩.你选谁?请说明理由.
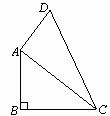
21、(本小题满分8分)已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17。试求:
(1)AC的长;
(2)四边形ABCD的面积;
22、(本小题满分10分)温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(°F),设摄氏温度为x(℃),华氏温度为y(°F),且y是x的一次函数.
(1)仔细观察图中数据,试求出y与x之间的函数表达式;
(2)当摄氏温度为

23、(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°将Rt△ABC绕点C顺时针方向旋转60°得到△DEC点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF连接AD.
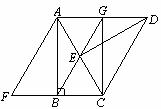
(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于G连接CG,请问:四边形ABCG是什么特殊平行四边形?为什么?
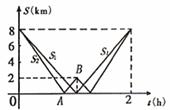
24、(本小题满分10分)在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),下图中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
四、实践与探索(本大题只有1小题,满分12分. 只要你开动脑筋,勇于探索,你一定会获得成功!)
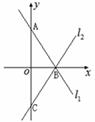
25、已知,如图,直线 :
: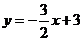 与
与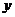 轴交于点
轴交于点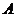 ,与直线
,与直线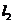 交于
交于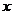 轴上同一点
轴上同一点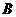 ,直线
,直线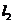 交
交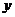 轴于点
轴于点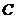 ,且点
,且点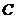 与点
与点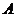 关于
关于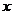 轴对称.
轴对称.
(1)求直线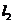 的解析式.
的解析式.
(2)若点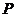 是直线
是直线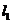 上任意一点,求证:点
上任意一点,求证:点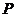 关于
关于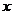 轴的对称点
轴的对称点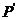 一定在直线
一定在直线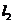 上.
上.
(3)设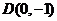 ,平行于
,平行于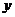 轴的直线
轴的直线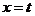 分别交直线
分别交直线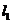 和
和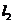 于点
于点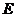 、
、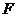 . 是否存在
. 是否存在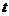 的值,使得以
的值,使得以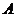 、
、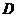 、
、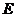 、
、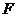 为顶点的四边形是平行四边形,若存在,求出
为顶点的四边形是平行四边形,若存在,求出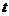 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.