摘要：(3)设.平行于轴的直线分别交直线和于点.. 是否存在的值.使得以...为顶点的四边形是平行四边形.若存在.求出的值,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu_id_774467[举报]
如图直线y=-x+10与x轴、y轴分别交于A、B两点，动点P从A点开始在线段AO上以每秒2个长度单位的速度向原点O运动．动直线EF从x轴开始以每秒1个长度单位的速度向上平行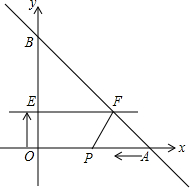
移动（即EF∥x轴），并且分别与y轴、线段AB交于E、F点．（当A运动到点O时，动直线EF随之停止运动） 连接FP，设动点P与动直线EF同时出发，运动时间为t秒．
（1）当t=1秒时，求△APF的面积；
（2）设t的值分别取t1、t2时（t1≠t2），所对应的三角形分别为△AF1P1和△AF2P2．试判断这两个三角形是否相似，请证明你的判断；
（3）t为何值时，梯形OPFE的面积最大，最大面积是多少？
查看习题详情和答案>>
移动（即EF∥x轴），并且分别与y轴、线段AB交于E、F点．（当A运动到点O时，动直线EF随之停止运动） 连接FP，设动点P与动直线EF同时出发，运动时间为t秒．（1）当t=1秒时，求△APF的面积；
（2）设t的值分别取t1、t2时（t1≠t2），所对应的三角形分别为△AF1P1和△AF2P2．试判断这两个三角形是否相似，请证明你的判断；
（3）t为何值时，梯形OPFE的面积最大，最大面积是多少？
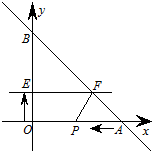如图，直线y=-x+20与x轴、y轴分别交于A、B两点，动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动．动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于E、F点．连接FP，设动点P与动直线EF同时出发，运动时间为t秒．（1）当t=1秒时，求梯形OPFE的面积．
（2）t为何值时，梯形OPFE的面积最大，最大面积是多少？
（3）设t的值分别取t1、t2时（t1≠t2），所对应的三角形分别为△AF1P1和△AF2P2．试判断这两个三角形是否相似，请证明你的判断． 查看习题详情和答案>>
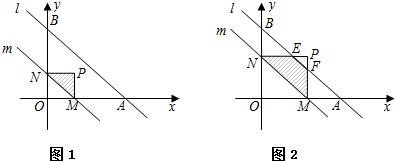
如图，直线l的解析式为y=-x+4，它与x轴、y轴分别相交于A、B两点．平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴、y轴分别相交于M、N两点，设运动时间为t秒（0＜t≤4）．
（1）求A、B两点的坐标；
（2）以MN为对角线作矩形OMPN，记△MPN和△OAB重合部分的面积为S1，在直线m的运动过程中，当t为何值时，S1为△OAB面积的
？
查看习题详情和答案>>
（1）求A、B两点的坐标；
（2）以MN为对角线作矩形OMPN，记△MPN和△OAB重合部分的面积为S1，在直线m的运动过程中，当t为何值时，S1为△OAB面积的
| 5 | 16 |
查看习题详情和答案>>
如图，直线y=-x+20与x轴、y轴分别交于A、B两点，动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动．动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动（即EF∥x轴），且分别与y轴、线段AB交于E、F点，当P点到达O点时，点P和直线EF均停止运动．连结FP，设动点P与动直线EF同时出发，运动时间为t秒．（1）当t=1秒时，求梯形OPFE的面积．
（2）t为何值时，梯形OPFE的面积最大，最大面积是多少？
如图，直线l1：y=-x+8与x轴、y轴分别交于点A和点B，直线l2：y=x与直线l1交于点C，平行于y轴的直线m从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点时停止．直线m交线段BC、OC于点D、E，以DE为斜边向左侧作等腰Rt△DEF，设△DEF与△BCO重叠部分的面积为S（平方单位），直线m的运动时间为t（秒）．
（1）填空：OA=
（2）填空：动点E的坐标为（t，
（3）求S与t的函数关系式并写出自变量的取值范围；
（4）设直线m与OA交于点P，是否存在这样的点P，使得P、O、F为顶点的三角形为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．
查看习题详情和答案>>
（1）填空：OA=
8
8
，∠OAB=45°
45°
；（2）填空：动点E的坐标为（t，
t
t
），DE=8-2t
8-2t
（用含t的代数式表示）；（3）求S与t的函数关系式并写出自变量的取值范围；
（4）设直线m与OA交于点P，是否存在这样的点P，使得P、O、F为顶点的三角形为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．