陕西省师大附中08-09学年高二下学期期中考试高二年级数学《选修2-2》试题
命题人:王全 审题人:李涛
一、选择题(10×4′=40′)
1.若函数 ,则
,则
A. B.
B.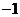 C.
C. D.
D.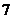
2.若复数 满足
满足 ,则
,则
A.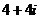 B.
B. C.
C. D.
D.
3.若随机变量ξ的分布列为:
ξ
4
X
9
10
P
0.3
0.1
Y
0.2
则Y的值为
 4.用数学归纳法证明:
4.用数学归纳法证明: (
(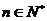 )能被
)能被 整除.从假设
整除.从假设 成立到
成立到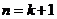 成立时,被整除式应为
成立时,被整除式应为
A.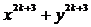 B.
B. C.
C. D.
D. 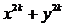
5.若 恒成立,则
恒成立,则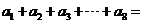
A.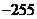 B.
B. C.
C.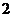 D.
D.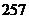
6.与直线 平行的抛物线
平行的抛物线 的切线方程为
的切线方程为
A. B.
B.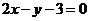 C.
C. D.
D.
7.用数字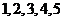 组成无重复数字的五位数,则
组成无重复数字的五位数,则 相邻,而
相邻,而 不相邻的数有
不相邻的数有
A.12个 B.24个 C.36个 D.48个
8.由直线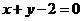 ,曲线
,曲线 以及
以及 轴围成的图形的面积为
轴围成的图形的面积为
A. B.
B.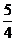 C.
C. D.
D.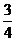
9.函数 ,
, 的最大值为
的最大值为
A.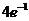 B.
B. C.
C.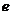 D.
D.
10.在数列 中,若
中,若 ,
, ,则
,则
A. B.
B.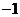 C.
C. D.
D.
二、填空题(4×4′=16′)
11.若函数 ,则
,则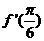 的值为 ___.
的值为 ___.
12.某人射击一次击中目标的概率为 .经过
.经过 次射击,此人恰有两次击中目标
次射击,此人恰有两次击中目标
的概率为 ___.
 13.函数
13.函数 的单调递增区间为
___.
的单调递增区间为
___.
14.若从集合 中任取三个不同的元素,则所取的三个元素可以构成等差数列的概率为 ___(填具体数值).
中任取三个不同的元素,则所取的三个元素可以构成等差数列的概率为 ___(填具体数值).
陕西省师大附中08-09学年高二下学期期中考试
高二年级数学答案
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
C
C
B
A
B
D
D
C
二、填空题(4×4′=16′)
11.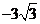 12.
12. 也可是
也可是 13.
13.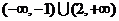 14.
14.
三、解答题(2×10′+2×12′=44′)
15.将五名志愿者随机地分到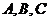 三个不同的岗位服务,每个岗位至少有一名志愿者.
三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求恰有两名志愿者参加 岗位服务的概率;
岗位服务的概率;
(2)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,求
岗位服务的人数,求 的分布列.
的分布列.
解: 将五名志愿者随机地分到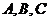 三个不同的岗位服务的基本事件总数为
三个不同的岗位服务的基本事件总数为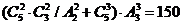 .
.
(1)记恰有两名志愿者参加 岗位服务为事件
岗位服务为事件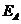 ,则
,则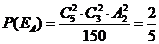 ,即恰有两名志愿者参加
,即恰有两名志愿者参加 岗位服务的概率是
岗位服务的概率是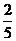 .
.
(2)由题意知随机变量 可能取的值为1,2,3,
可能取的值为1,2,3, 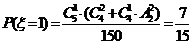 ;
;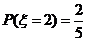 ,
, ,所以
,所以 的分布列是
的分布列是
ξ
1
2
3
P
7/15
2/5
2/15
16.已知函数 在
在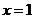 处取得极值
处取得极值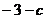 ,
,
 (1)试求实数
(1)试求实数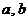 的值;
的值;
(2)试求函数 的单调区间;
的单调区间;
(3)若对任意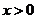 ,不等式
,不等式 恒成立,求实数
恒成立,求实数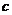 的取值范围.
的取值范围.
解:(1)由题意知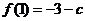

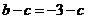 ,∴
,∴ ;对
;对 求导可得:
求导可得:
 .由题意,得
.由题意,得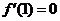 ,即
,即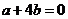 , ∴
, ∴ ;即实数
;即实数 ,
, .
.
(2)由(1)知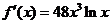
 ,令
,令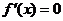 ,解得
,解得 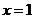 ,
,
当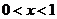 时,
时,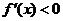 ,此时
,此时 为减函数;
为减函数;
当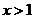 时,
时,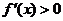 ,此时
,此时 为增函数.
为增函数.
∴函数 的单调递减区间为
的单调递减区间为 ,
, 的单调递增区间为
的单调递增区间为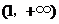 ;
;
(3)由(2)知, 在
在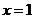 处取得极小值
处取得极小值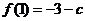 ,此极小值也是最小值,要使
,此极小值也是最小值,要使 (
(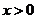 )恒成立,只需
)恒成立,只需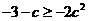 ,
,
即
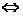
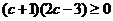 ,解得
,解得 , 或
, 或 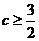 .
.
∴实数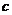 的取值范围为
的取值范围为 .
.
17.设数列 的前
的前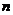 项和为
项和为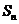 ,且对
,且对 都有
都有 ,则:
,则:
(1)求数列 的前三项
的前三项 ;
;
(2)求数列 的通项
的通项 ,并说明理由;
,并说明理由;
 (3)求证:对任意
(3)求证:对任意 都有
都有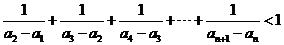 .
.
解: (1)令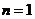 得,
得, ,故
,故 ;
;
令 得,
得, ,故
,故 ;
;
令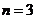 得,
得, ,故
,故 ;
;
(2)由(1)可以猜想 ,下面用数学归纳法进行证明:
,下面用数学归纳法进行证明:
①当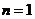 时,结论显然成立;
时,结论显然成立;
②假设当 时结论成立,即
时结论成立,即 ,从而由已知
,从而由已知 可得:
可得: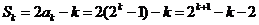 .故
.故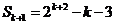 .
.
∴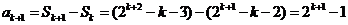 .
.
即,当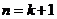 时结论成立.
时结论成立.
综合①②可知,猜想 成立.即,数列
成立.即,数列 的通项为
的通项为 .
.
(3)∵ ,∴
,∴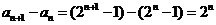 ,
,
∴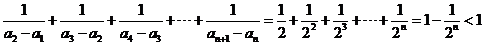
∴对任意 都有
都有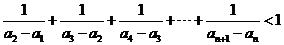 .
.
18.在直线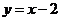 上是否存在点
上是否存在点 ,使得经过点
,使得经过点 能作出抛物线
能作出抛物线 的两条互相垂直的切线?若存在,求点
的两条互相垂直的切线?若存在,求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

 解:假设这样的点P存在,由题意可设点P坐标为
解:假设这样的点P存在,由题意可设点P坐标为 ,又设所作的两条切线为PA,PB,其中A,B为切点,且点A,B的坐标分别为:
,又设所作的两条切线为PA,PB,其中A,B为切点,且点A,B的坐标分别为:
 ,
,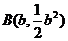 .
.
因为函数 的导函数为
的导函数为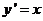 ,
,
所以由两切线垂直可得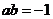 ,且:
,且:

即,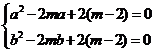 . 故
. 故 是方程
是方程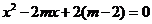 的两实数根,
的两实数根,
从而有: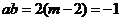 . 解得:
. 解得: .
.
所以,存在这样的点P,其坐标为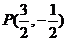 .
.
高二年级数学答题纸
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题(4×4′=16′)
11._________ 12._________ 13._________ 14._________
三、解答题(2×10′+2×12′=44′)
15.将五名志愿者随机地分到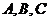 三个不同的岗位服务,每个岗位至少有一名志愿者.
三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求恰有两名志愿者参加 岗位服务的概率;
岗位服务的概率;
(2)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,求
岗位服务的人数,求 的分布列.
的分布列.
16.已知函数 在
在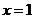 处取得极值
处取得极值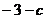 ,
,
(1)试求实数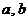 的值;
的值;
(2)试求函数 的单调区间;
的单调区间;
(3)若对任意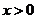 ,不等式
,不等式 恒成立,求实数
恒成立,求实数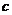 的取值范围.
的取值范围.
17.设数列 的前
的前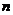 项和为
项和为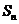 ,且对
,且对 都有
都有 ,则:
,则:
(1)求数列 的前三项
的前三项 ;
;
(2)求数列 的通项
的通项 ,并说明理由;
,并说明理由;
(3)求证:对任意 都有
都有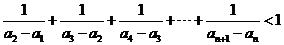 .
.
18.在直线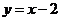 上是否存在点
上是否存在点 ,使得经过点
,使得经过点 能作出抛物线
能作出抛物线 的两条互相垂直的切线?若存在,求点
的两条互相垂直的切线?若存在,求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

