网址:http://m.1010jiajiao.com/timu_id_53130[举报]
函数![]() 的定义域为(0,1](a为实数)
的定义域为(0,1](a为实数)
(1)当a=-1时,求函数y=f(x)的值域;
(2)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(3)求函数y=f(x)在(0,1]上的最大值及最小值,并求出此时x的值.
若函数 同时满足下列条件,(1)在D内为单调函数;(2)存在实数
同时满足下列条件,(1)在D内为单调函数;(2)存在实数 ,
,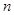 .当
.当 时,
时, ,则称此函数为D内的等射函数,设
,则称此函数为D内的等射函数,设
 则:
则:
(1)  在(-∞,+∞)的单调性为 (填增函数或减函数);(2)当
在(-∞,+∞)的单调性为 (填增函数或减函数);(2)当 为R内的等射函数时,
为R内的等射函数时, 的取值范围是
.
的取值范围是
.
查看习题详情和答案>>
若函数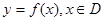 同时满足下列条件,(1)在D内为单调函数;(2)存在实数
同时满足下列条件,(1)在D内为单调函数;(2)存在实数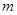 ,
,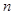 .当
.当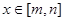 时,
时,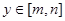 ,则称此函数为D内的等射函数,设
,则称此函数为D内的等射函数,设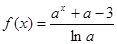
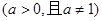 则:
则:
(1)  在(-∞,+∞)的单调性为 (填增函数或减函数);(2)当
在(-∞,+∞)的单调性为 (填增函数或减函数);(2)当 为R内的等射函数时,
为R内的等射函数时,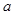 的取值范围是 .
的取值范围是 .
设函数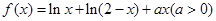 .
.
(Ⅰ) 当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
【解析】第一问中利用函数 的定义域为(0,2),
的定义域为(0,2), .
.
当a=1时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
第二问中,利用当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数 的定义域为(0,2),
的定义域为(0,2), .
.
(1)当 时,
时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
(2)当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
查看习题详情和答案>>
设函数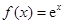 ,其中
,其中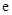 为自然对数的底数.
为自然对数的底数.
(1)求函数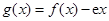 的单调区间;
的单调区间;
(2)记曲线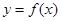 在点
在点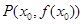 (其中
(其中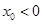 )处的切线为
)处的切线为 ,
, 与
与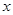 轴、
轴、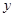 轴所围成的三角形面积为
轴所围成的三角形面积为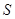 ,求
,求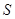 的最大值.
的最大值.
【解析】第一问利用由已知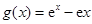 ,所以
,所以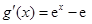 ,
,
由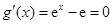 ,得
,得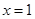 ,
所以,在区间
,
所以,在区间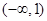 上,
上,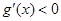 ,函数
,函数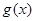 在区间
在区间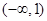 上单调递减;
在区间
上单调递减;
在区间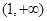 上,
上, ,函数
,函数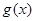 在区间
在区间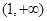 上单调递增;
上单调递增;
第二问中,因为 ,所以曲线
,所以曲线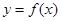 在点
在点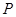 处切线为
处切线为 :
: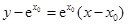 .
.
切线 与
与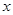 轴的交点为
轴的交点为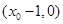 ,与
,与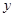 轴的交点为
轴的交点为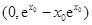 ,
,
因为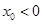 ,所以
,所以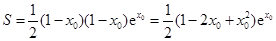 ,
,
 , 在区间
, 在区间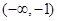 上,函数
上,函数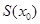 单调递增,在区间
单调递增,在区间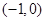 上,函数
上,函数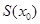 单调递减.所以,当
单调递减.所以,当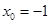 时,
时,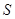 有最大值,此时
有最大值,此时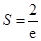 ,
,
解:(Ⅰ)由已知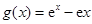 ,所以
,所以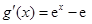 ,
由
,
由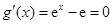 ,得
,得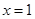 , 所以,在区间
, 所以,在区间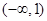 上,
上,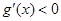 ,函数
,函数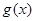 在区间
在区间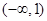 上单调递减;
上单调递减;
在区间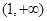 上,
上, ,函数
,函数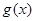 在区间
在区间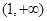 上单调递增;
上单调递增;
即函数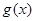 的单调递减区间为
的单调递减区间为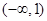 ,单调递增区间为
,单调递增区间为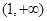 .
.
(Ⅱ)因为 ,所以曲线
,所以曲线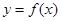 在点
在点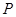 处切线为
处切线为 :
: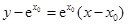 .
.
切线 与
与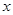 轴的交点为
轴的交点为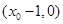 ,与
,与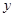 轴的交点为
轴的交点为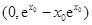 ,
,
因为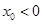 ,所以
,所以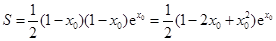 ,
,
 , 在区间
, 在区间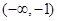 上,函数
上,函数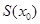 单调递增,在区间
单调递增,在区间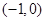 上,函数
上,函数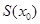 单调递减.所以,当
单调递减.所以,当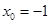 时,
时,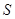 有最大值,此时
有最大值,此时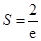 ,
,
所以,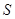 的最大值为
的最大值为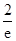
查看习题详情和答案>>