2009年四川省达州市高中阶段教育学校招生统一考试
数学试卷
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至10页.考试时间100分钟,满分100分.
第Ⅰ卷 (选择题 共24分)
1.答第Ⅰ卷前,考生务必将姓名、准考证号、考试科目按要求填涂在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题号的答案标号涂黑,不能将答案答在试题卷上.
3.考试结束,将本试卷和答题卡一并交回.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本题8小题,每小题3分,共24分)
1.下列各数中,最小的数是
A.-1 B. -
2.下列计算正确的是
A.a+ B.
B.
C.a
 a
a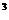 =a
=a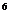 D.
D.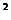 ÷
÷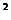 =
=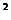
3.在一次环保知识问答中,一组学生成绩统计如下:
分数
50
60
70
80
90
100
人数
1
4
9
15
16
5
则该组学生成绩的中位数是
A.70 B.
4. 如图1,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,以下四个结论:①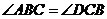 ,②OA=OD ,③
,②OA=OD ,③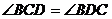 ,④S
,④S =S
=S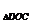 ,其中正确的是
,其中正确的是
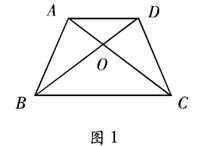
A. ①② B.①④ C.②③④ D.①②④
5.函数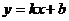 的图象如图2所示,则当y<0时,
的图象如图2所示,则当y<0时, 的取值范围是
的取值范围是
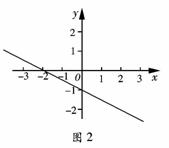
A.  <-2 B.
<-2 B.  >-2 C.
>-2 C.  <-1 D.
<-1 D.  >-1
>-1
6. 在平面直角坐标系中,设点P到原点O的距离为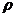 ,OP与x轴正方向的夹角为
,OP与x轴正方向的夹角为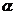 ,则用
,则用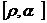 表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为
表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为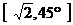 .若点Q的极坐标为
.若点Q的极坐标为 ,则点Q的坐标为
,则点Q的坐标为
A.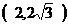 B.
B. C.(2
C.(2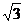 ,2) D.(2,2)
,2) D.(2,2)
7.图3是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
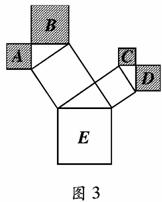
A.13 B.26 C.47 D.94
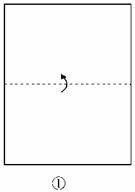
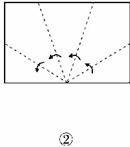
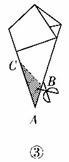
8.跟我学剪五角星:如图4,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36 ),则在图③中应沿什么角度剪?即∠ABC的度数为
),则在图③中应沿什么角度剪?即∠ABC的度数为

A.126 B.108
B.108 C.90
C.90 D.72
D.72
第Ⅱ卷 (非选择题 共76分)
二、填空题:把最后答案直接填在题中的横线上(本题7小题,每小题3分,共21分).
9、分解因式:mn -m=_______________________.
-m=_______________________.
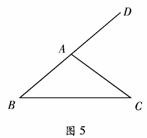
10、如图5,△ABC中,AB=AC,与∠BAC相邻的外角为80°,则∠B=____________.
11、若a-b=1,ab=-2,则(a+1)(b-1)=___________________.
12、将一种浓度为15ㄇ的溶液30┧,配制成浓度不低于20ㄇ的同种溶液,则至少需要浓度为35ㄇ的该种溶液____________┧.
13、长度为2┩、3┩、4┩、5┩的四条线段,从中任取三条线段能组成三角形的概率是______________.
14、达成铁路扩能改造工程将于今年6月底完工,届时达州至成都运营长度约为350千米,若一列火车以170千米/时的平均速度从达州开往成都,则火车距成都的路程y(千米)与行驶时间(时)之间的函数关系式为__________________.
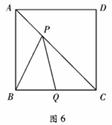
15、如图6,在边长为2┩的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为____________┩(结果不取近似值).
(一)(本题2小题,共13分)
三、解答题:解答时应写出必要的文字说明、证明过程或演算步骤(55分)
16.(8分)
(1)(4分)计算:(-1)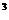 +(2009-
+(2009- )
)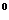 -
-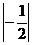
(2)(4分)解不等式组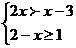 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
不等式组的解集在数轴上表示如下:
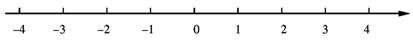
17.(6分)在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:
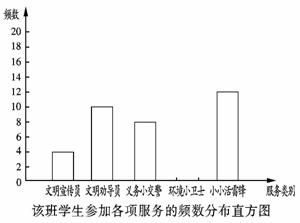
该班学生参加各项服务的频数、频率统计表
服务类别
频数
频率
文明宣传员
4
0.08
文明劝导员
10
义务小交警
8
0.16
环境小卫士
0.32
小小活雷锋
12
0.24
请根据上面的统计图表,解答下列问题:
(1)该班参加这次公益活动的学生共有____________名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.
(二)(本题2小题,共11分)
18.(5分)如图7,在△ABC中,AB=2BC,点D、点E分别为AB、AC的中点,连结DE,将△ADE绕点E旋转180 得到△CFE.试判断四边形BCFD的形状,并说明理由.
得到△CFE.试判断四边形BCFD的形状,并说明理由.

19.(6分)如图8,直线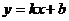 与反比例函数
与反比例函数 (
(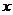 <0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.

(1)试确定反比例函数的关系式;
(2)求△AOC的面积.
(三)(本题2小题,共13分)
20.(6分)阳光明媚的一天,数学兴趣小组的同学去操场上测量旗杆的高度,他们带了以下测量工具:皮具、三角尺、标杆、小平面镜等.
首先,小明说:“我们用皮尺和三角尺(含30 角)来测量”.于是大家一起动手,测得小明与旗杆的距离AC为15┩,小明的眼睛与地面的距离为1.6┩,如图9(甲)所示.
角)来测量”.于是大家一起动手,测得小明与旗杆的距离AC为15┩,小明的眼睛与地面的距离为1.6┩,如图9(甲)所示.
然后,小红和小强提出了自己的想法.
小红说:“我用皮尺和标杆能测出旗杆的高度.”
小强说:“我用皮尺和小平面镜也能测出旗杆的高度!”
根据以上情景,解答下列问题:
(1)利用图9(甲),请你帮助小明求出旗杆AB的高度(结果保留整数.参考数据: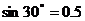 ,
,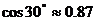 ,
,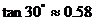 ,
,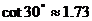 );
);
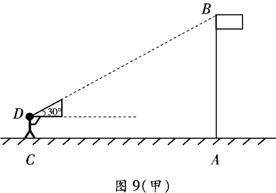
(2)你认为小红和小强提出的方案可行吗?如果可行,请选择一中方案在图9(乙)中画出测量示意图,并简述测量步骤.
21、(7分)某学生食堂存煤45吨,用了5天后,由于改进设备,平均每天耗煤量降低为原来的一半,结果多烧了10天.
(1)求改进设备后平均每天耗煤多少吨?
(2)试将该题内容改编为与我们日常生活、学习有关的问题,使所列的方程相同或相似(不必求解).
(四)(本题2小题,共17分)
22.(8分)如图10,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
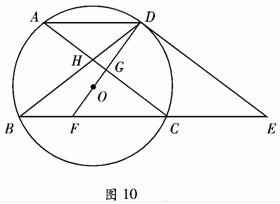
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5┩,AC=8┩,求⊙O的半径.
23、(9分)如图11,抛物线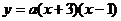 与
与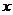 轴相交于A、B两点(点A在点B右侧),过点A的直线交抛物线于另一点C,点C的坐标为(-2,6).
轴相交于A、B两点(点A在点B右侧),过点A的直线交抛物线于另一点C,点C的坐标为(-2,6).
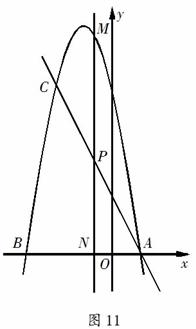
(1)求a的值及直线AC的函数关系式;
(2)P是线段AC上一动点,过点P作y轴的平行线,交抛物线于点M,交x轴于点N.
①求线段PM长度的最大值;
②在抛物线上是否存在这样的点M,使得△CMP与△APN相似?如果存在,请直接写出所有满足条件的点M的坐标(不必写解答过程);如果不存在,请说明理由.