2009届浙江省义乌市初中毕业生学业考试
数学试卷
考生须知:
1.全卷共4页,有3大题,24小题。满分为120分。考试时间120分钟.
2.本卷答案必须做在答题纸的对应位置上,做在试卷上无效。
3.请考生将姓名、准考生号填写在答题纸的对应位置上,并认真核准条形码的姓名、准考证号。
4.作图时,可先使用2B铅笔,确定后必须使用0.5毫米及以上的黑色签字笔涂黑。
温馨提示:请仔细审题,细心答题,相信你一定会有出色的表现!
参考公式:二次函数 图像的顶点坐标是
图像的顶点坐标是
试卷Ⅰ
说明:本卷共有1大题,10小题,每小题3分,共30分.请使用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满。
一、选择题(请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.在实数0,1, ,0.1235中,无理数的个数为
,0.1235中,无理数的个数为
A.0个 B.1个 C.2个 D.3个
2.尽管受到国际金融危机的影响,但义乌市经济依然保持了平稳增长。据统计,截止到今年4月底,我市金融机构存款余额约为1193亿元,用科学计数法应记为
A.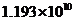 元
B.
元
B.  元
元
C. 元
D.
元
D.  元
元
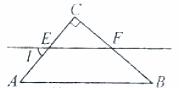
3.如图,在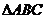 中,
中,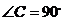 ,EF//AB,
,EF//AB, ,则
,则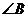 的度数为
的度数为
A. B.
B.  C.
C. D.
D. 
4.下列由若干个单位立方体搭成的几何体中,左视图是图1的为
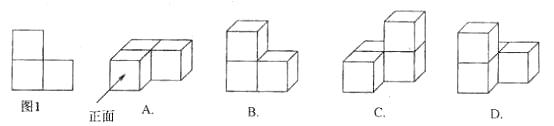
A.12.
6.下列事件是必然事件的
A.抛掷一枚硬币,四次中有两次正面朝上
B.打开电视体育频道,正在播放NBA球赛
C.射击运动员射击一次,命中十环
D.若a是实数,则
7.在正三角形、正方形、正五边形、正六边形中不能单独镶嵌平面的是
A.正三角形 B.正方形
C.正五边形 D.正六边形
8.下列调查适合作抽样调查的是
A.了解义乌电视台“同年哥讲新闻”栏目的收视率
B.了解某甲型H1N1确诊病人同机乘客的健康状况
C.了解某班每个学生家庭电脑的数量
D.“神七”载人飞船发射前对重要零部件的检查
9.如图,一块砖的外侧面积为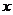 ,那么图中残留部分墙面的面积为
,那么图中残留部分墙面的面积为

A. A.
A. A.
A. A.
A.
10.同时抛掷两枚质地均匀的骰子,骰子的六个面分别刻有1到6的点数,朝上的面的点数中,一个点数能被另一个点数整除的概率是
A.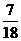 B.
B. C.
C.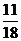 D.
D.
试卷Ⅱ
说明:本卷共有2大题,14小题,共90分。答题请用0.
二、填空题(本题有6小题),每小题4分,共24分)
11.化简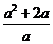 的结果是_________
的结果是_________
12.不等式组
 的解是______________
的解是______________
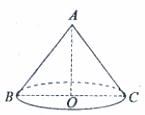
13.如图,圆锥的侧面积为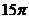 ,底面半径为3,则圆锥的高AO为_________
,底面半径为3,则圆锥的高AO为_________
 ⊙
⊙
14.平方根节是数学爱好者的节目,这一天的月份和日期的数字正好是当年年份最后两位数字的平方根,例如2009年的
_________年__________月__________日。
15.已知,点 是反比例函数
是反比例函数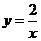 图像上的一个动点,⊙
图像上的一个动点,⊙ 的半径为1,当⊙
的半径为1,当⊙ 与坐标轴相交时,点
与坐标轴相交时,点 的横坐标
的横坐标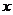 的取值范围是___________
的取值范围是___________
16.如图,抛物线 与
与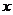 轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则
轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则

 __________
__________ (填“
(填“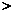 ”或“
”或“ ”);
”);
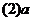 的取值范围是__________
的取值范围是__________
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)计算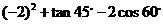 ;
;
(2)解方程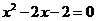 。
。
18.如图,在边长为4的正三角形ABC中,AD BC于点D,以AD为一边向右作正三角形ADE。
BC于点D,以AD为一边向右作正三角形ADE。

(1)求△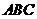 的面积S;
的面积S;
(2)判断AC、DE的位置关系,并给出证明。
19.
(1)如图1,正方形网格中有一个平行四边形,请在图1中画一条直线把平行四边形分成面积相等的两部分;
(2)把图2中的平行四边形分割成四个全等的四边形(要求在图2中画出分割线),并把所得的四个全等的四边形在图3中拼成一个轴对称图形或中心对称图形,使所得图形与原图形不全等且各个顶点都落在格点上。
温馨提示:作图时,可先使用2B铅笔,确定后必须使用0.

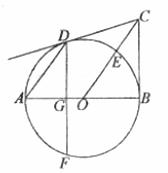
20.如图,AB是⊙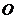 的直径,BC
的直径,BC AB于点B,连接OC交⊙
AB于点B,连接OC交⊙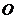 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF AB于点G。
AB于点G。
(1)求证:点E是 的中点;
的中点;
(2)求证:CD是⊙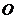 的切线;
的切线;
(3)若 ,⊙
,⊙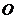 的半径为5,求DF的长。
的半径为5,求DF的长。
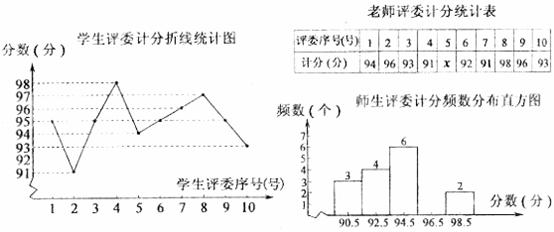
21.五月花海,歌声飘扬,2009年5月,义乌市各中小学举行了 “班班有歌声”活动,某校比赛聘请了10位老师和10位学生担任评委,其中甲班的得分情况如下统计图(表)所示。
(1)在频数分布直方图中,自左向右第四组的频数为_____;
(2)学生评委计分的中位数是_____分;
(3)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分, 的值。
的值。
22.据统计,2008年底义乌市共有耕地267000亩,户籍人口724000人,2004年底至2008年底户籍人口平均每两年约增加2%,假设今后几年继续保持这样的增长速度。(本题计算结果精确到个位)
(1)预计2012年底义乌市户籍人口约多少人?
(2)为确保2012年底义乌市人均耕地面积不低于现有水平,预计2008年底至2012年底平均每年耕地总面积至少应该增加多少亩?
23.如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP= ,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原。
,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原。
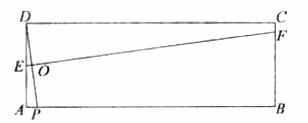
(1)当 时,折痕EF的长为__________;当点E与点A重合时,折痕EF的长为_________;
时,折痕EF的长为__________;当点E与点A重合时,折痕EF的长为_________;
(2)请写出使四边形EPFD为菱形的 的取值范围,并求出当
的取值范围,并求出当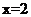 时菱形的边长;
时菱形的边长;
(3)令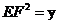 ,当点E在AD、点F在BC上时,写出
,当点E在AD、点F在BC上时,写出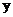 与
与 的函数关系式。当
的函数关系式。当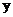 取最大值时,判断△
取最大值时,判断△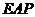 与△
与△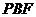 是否相似?若相似,求出
是否相似?若相似,求出 的值;若不相似,请说明理由。
的值;若不相似,请说明理由。
温馨提示:用草稿纸折折看,或许对你有所帮助哦!

24.已知点A、B分别是 轴、
轴、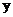 轴上的动点,点C、D是某个函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。例如:如图,正方形ABCD是一次函数
轴上的动点,点C、D是某个函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。例如:如图,正方形ABCD是一次函数 图像的其中一个伴侣正方形。
图像的其中一个伴侣正方形。
(1)若某函数是一次函数 ,求它的图像的所有伴侣正方形的边长;
,求它的图像的所有伴侣正方形的边长;
(2)若某函数是反比例函数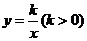 ,他的图像的伴侣正方形为ABCD,点D(2,m)(m <2)在反比例函数图像上,求m的值及反比例函数解析式;
,他的图像的伴侣正方形为ABCD,点D(2,m)(m <2)在反比例函数图像上,求m的值及反比例函数解析式;
(3)若某函数是二次函数 ,它的图像的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_________,写出符合题意的其中一条抛物线解析式_______,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?___________。(本小题只需直接写出答案)
,它的图像的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_________,写出符合题意的其中一条抛物线解析式_______,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?___________。(本小题只需直接写出答案)
