摘要：(3)令.当点E在AD.点F在BC上时.写出与的函数关系式.当取最大值时.判断△与△是否相似?若相似.求出的值,若不相似.请说明理由.温馨提示:用草稿纸折折看.或许对你有所帮助哦!
网址：http://m.1010jiajiao.com/timu_id_754769[举报]
如图，在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．
（1）当x=0时，折痕EF的长为 ；当点E与点A重合时，折痕EF的长为 ；
（2）请写出使四边形EPFD为菱形的x的取值范围，并求出当x=2时菱形的边长；
（3）令EF2=y，当点E在AD、点F在BC上时，写出y与x的函数关系式．当y取最大值时，判断△EAP与△PBF是否相似？若相似，求出x的值；若不相似，请说明理由．温馨提示：用草稿纸折折看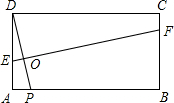
，或许对你有所帮助哦！
查看习题详情和答案>>
（1）当x=0时，折痕EF的长为
（2）请写出使四边形EPFD为菱形的x的取值范围，并求出当x=2时菱形的边长；
（3）令EF2=y，当点E在AD、点F在BC上时，写出y与x的函数关系式．当y取最大值时，判断△EAP与△PBF是否相似？若相似，求出x的值；若不相似，请说明理由．温馨提示：用草稿纸折折看
，或许对你有所帮助哦！
查看习题详情和答案>>
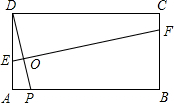
如图，在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．（1）当点E与点A重合时，折痕EF的长为
（2）写出使四边形EPFD为菱形的x的取值范围，并求出当x=2时菱形的边长；
（3）令EF2=y，当点E在AD、点F在BC上时，写出y与x的函数关系式（写出x的取值范围）． 查看习题详情和答案>>
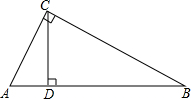（2013•甘井子区二模）如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AC=| 5 |
| 5 |
（1）画出△AC1D1；
（2）当点D2落在BC上时，t的值为
3.5
3.5
秒；（3）令△A1C2D2与△BCD的重叠面积为S，求出S与t之间的函数关系式，并写出相应的自变量t的取值范围．
如图，在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．
，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原
。
时，折痕EF的长为( )；当点E与点A重合时，折痕EF的长为( )；
时菱形的边长；
，当点E在AD、点F在BC上时，写出
与
与
是否相似？若相似，求出