2008-2009学年度淄博市张店第一学期初四期末学业水平测试
数学试卷
一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,每小题3分,共36分,错选、不选或选出的答案超过一个,均记0分)
1.如下图,在Rt△ABC中,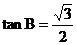 ,
,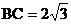 ,则AC等于
,则AC等于
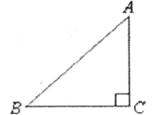
A.3 B.4 C.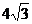 D.6
D.6
2.把抛物线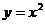 向右平移2个单位得到的抛物线是
向右平移2个单位得到的抛物线是
A.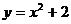 B.
B.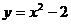 C.
C.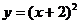 D.
D.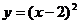
3.二次函数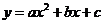
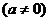 的图像如下图所示,当
的图像如下图所示,当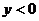 时,
时,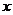 的取值范围是
的取值范围是
A. B.
B.
C.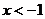 D.
D.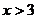 或
或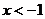
4.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是
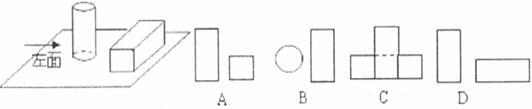
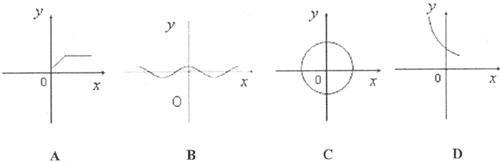
5.下列图形中的曲线不表示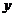 是
是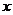 的函数的是
的函数的是
6.二次函数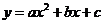
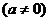 的图像如下图所示,则下列结论:①
的图像如下图所示,则下列结论:①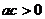 ;②
;②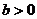 ;③
;③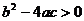 ,其中正确的个数是
,其中正确的个数是
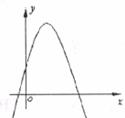
A.0个 B.1个 C.2个 D.3个
7.如下图,在⊙O中,AB是弦,OC⊥AB,垂足为C,若AB=16,OC=6,则⊙O的半径OA等于
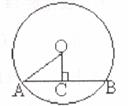
A.16 B.
8.下列说法正确的是
A.垂直于半径的直线是圆的切线 B.过三点A、B、C一定可以确定一个圆
C.平分弦的直径垂直于弦 D.相等的弦所对的弧不一定相等
9.一个函数的图像如下图,给出以下结论:
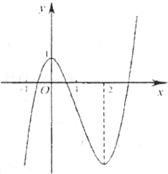
①当 时,函数值最大; ②当
时,函数值最大; ②当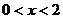 时,函数
时,函数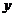 随
随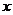 的增大而减小;
的增大而减小;
③存在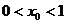 ,当
,当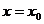 时,函数值为0。其中正确的结论是
时,函数值为0。其中正确的结论是
A.①② B.①③ C.②③ D.①②③
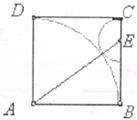
10.如下图,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则 的值为
的值为
A.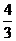 B.
B.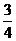 C.
C.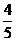 D.
D.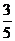
11.若同一个圆的内接正三角形、正方形、正六边形的边心距分别为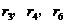 ,则
,则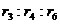 等于
等于
A.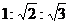 B.
B.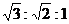 C.1┱2┱3 D.3┱2┱1
C.1┱2┱3 D.3┱2┱1
12.如下图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B时,人影长度
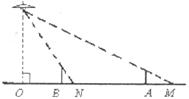
A.变长3.5米 B.变短3.5米 C.变长2.5米 D.变短2.5米
二、填空题(本题共5小题,满分20分,只要求填写最后结果,每小题填对,得4分)
13.一名滑雪运动员从坡比为1┱5的山坡上滑下.如果这名运动员滑行的距离是150米,那么他下滑的高度是_________米(用精确值表示)。
14.已知四边形ABCD内接于⊙O,且∠A┱∠C=1┱2,则∠BOD=_________。
15.二次函数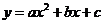 的部分对应值如下表:
的部分对应值如下表:
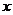
…
-3
-2
0
1
3
5
…
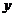
…
7
0
-8
-9
-5
7
…
二次函数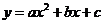 图像的对称轴为_______,
图像的对称轴为_______,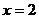 对应的函数值
对应的函数值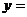 _______。
_______。
16.如下图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是_________。

17.如下图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=18°,则∠CDA=_________。
三、解答题(本大题共8小题,共64分。解答要写出必要的文字说明、证明过程或演算步骤)
18.计算(本题满分6分)

19.(本题满分6分)
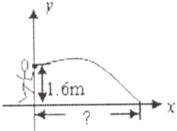
丁丁推铅球的出手高度为1.6
m,在下图所示的直角坐标系中,抛物线解析式为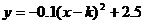 ,求铅球的落点与丁丁的距离。
,求铅球的落点与丁丁的距离。
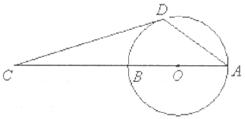
20.(本题满分8分)
已知:如图,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,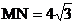 cm。
cm。
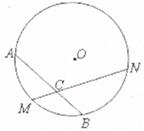
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数。
21.(本题满分8分)
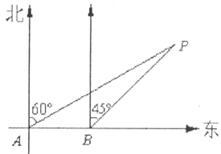
如下图,海上有一灯塔P,在它周围3海里处有暗礁。一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向。问客轮不改变方向继续前进有无触礁的危险?
22.(本题满分8分)
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱。
(1)求平均每天销售量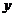 (箱)与销售价
(箱)与销售价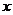 (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润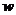 (元)与销售价(
(元)与销售价(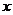 元/箱)之间的函数关系式;
元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
23.(本题满分8分)
如下图,已知二次函数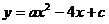 的图像经过点A和B。
的图像经过点A和B。
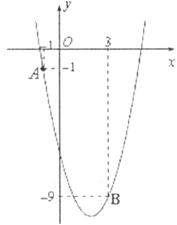
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P( )与点Q均在该函数图像上(其中
)与点Q均在该函数图像上(其中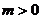 ),且这两点关于抛物线的对称轴对称,求
),且这两点关于抛物线的对称轴对称,求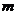 的值及点Q到
的值及点Q到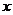 轴的距离。
轴的距离。
24.(本题满分10分)
如下图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米。⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径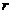 (厘米)与时间
(厘米)与时间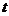 (秒)之间的关系式为
(秒)之间的关系式为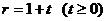 。
。

(1)试写出点A,B之间的距离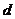 (厘米)与时间
(厘米)与时间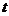 (秒)之间的函数表达式;
(秒)之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
25.(本题满分10分)
如下图所示,将△AOB置于平面直角坐标系中,其中点O为坐标原点,点A的坐标为(3,0),∠ABO=60°。
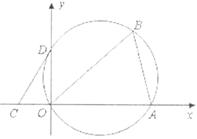
(1)若△AOB的外接圆与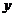 轴交于点D,求D点坐标。
轴交于点D,求D点坐标。
(2)若点C的坐标为(-1,0),试猜想过D,C的直线与△AOB的外接圆的位置关系,并加以说明。
(3)二次函数的图像经过点O和A且顶点在圆上,求此函数的解析式。