2008年河北省初中毕业生学业模拟考试(三)
数学试卷
本试卷满分为120分,考试时间为120分钟.
一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.sin45°的值是 ( )
A. B.
B.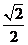 C.
C.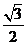 D.1
D.1
2.方程 的根是 ( )
的根是 ( )
A、2; B、-2; C、2或-2; D、以上答案都不对
3.当你走在路灯下,越来越接近路灯时,你的影子的长是如何变化( )
A、变长; B、变短; C、不变; D、无法确定
4.等腰三角形两边长分别为6、3,则该等腰三角形的周长为 ( )
A、15; B、12; C、12或15; D、9
5.如图,为了测量学校操场上旗杆BC的高度,在距旗杆
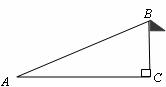
A.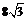 米 B、
米 B、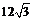 米 C、
米 C、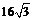 米 D、
米 D、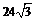 米
米
6.如图所示,正方形ABCD边长为2,点E在CB的延长线上, BD=BE,则tan∠BAE的值为 ( )
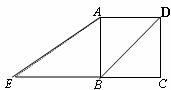
A、 ; B、1; C、
; B、1; C、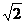 ; D、
; D、
7.如图,顺次连结四边形ABCD各中点得四边形EFGH,要使四边形EFGH为菱形,应添加的条件是( ).
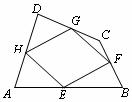
A.AB∥DC B.AB=DC
C.AC⊥BD D.AC=BD
8.如图所示,若将正方形分成k个全等的矩形,期中上、下各横排两个,中间竖排若干个,则k的值为 ( )
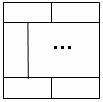
A、6; B、8; C、10; D、12
9.如图,P1、P2、P3是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形△P

A. S1<S2<S3 B. S2<S1<S
10.已知有一根长10为的铁丝,折成了一个矩形框。则这个矩形相邻两边 a、b之间函数的图象大至为 ( ).

二、填空题(每小题3分,共15分.把答案写在题中横线上)
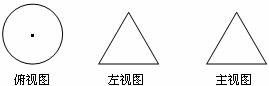
11.一几何体的三种视图如图所示,那么这个几何体是 ______ 。
12.若x=-1,是方程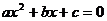 的一个根,则a、b、c满足 _________关系
的一个根,则a、b、c满足 _________关系
13.一个小正方体的6个面上的数字分别为1、2、3、4、5、6,抛出小正方体,小正方体落地后,面朝上的数字为偶数的概率是________。
14.抛物线 的顶点坐标是
______.
的顶点坐标是
______.
15.△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50º,则底角B为 ________ 度。
三、解答题(本大题共10个小题;共85分.解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分7分)
已知:某商场的
17.(本小题满分7分)
如图,已知:在平行四边形ABCD中,AB=

18.(本小题满分7分)
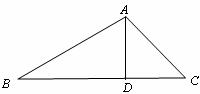
如图,已知:在△ABC中,AD是BC边上的高,∠B=30°,∠C=45°,BC=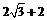 ,求AD的长。
,求AD的长。
19.(本小题满分8分)
如图,CD,EF表示高度不同的两座建筑物,已知CD高
∠FNM=30°,求AN之间的距离。

20.(本小题满分8分)
如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字。
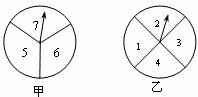
(1)用转盘上所指的两个数字作乘积,列举(用列表或画树状图)所有可能得到的数字之积;
(2)求出(1)中数字之积为奇数的概率。
21.(本小题满分8分)
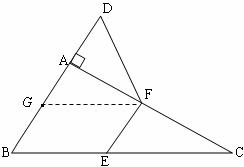
如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD= AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE。
AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE。
22.(本小题满分8分)
“自由落体”研究的是自由下落的物体下落时间(t)和下落高度(h)两个变量之间的变化规律.物理学家在当时反复实验、测量后得到下面的数据表:

为了进一步研究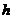 与
与 之间的函数关系,请你通过计算完成下表:
之间的函数关系,请你通过计算完成下表:
 (秒)
(秒)
1
2
3
4
5

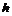 (米)
(米)
4.9
19.6
44.1
78.4
122.5

观察上面的数表,你发现 的值有什么变化规律吗? 请你写出用t表示h的表达式.
的值有什么变化规律吗? 请你写出用t表示h的表达式.
23.(本小题满分8分)
如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=
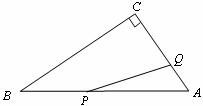
(1)用含t的代数式表示线段AP,AQ的长;
(2)当t为何值时△APQ是以PQ为底的等腰三角形?
(3)当t为何值时PQ∥BC?
24.(本小题满分12分)
如图1,E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上可以移动的四个点,每组对边上的两个点,可以连接成一条线段。
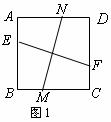
⑴如图2,如果EF∥BC, MN∥CD,那么EF MN(位置),EF MN(大小)
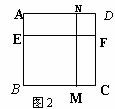
⑵如图3,如果E与A,F与C,M与B,N与D重合,那么EF MN(位置),EF MN(大小)
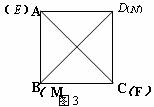
⑶当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时,猜想线段EF、MN满足什么位置关系时,才会有EF=MN,画出相应的图形,并证明你的猜想。
25.(本小题满分12分)
某计算机商店销售计算机,经统计每台售价9000元时,每天销售20台,而降价销售则销量增加,每台每降价300元,日销量增加一台,设日销量增加x台, 日销售额为y元
⑴用含x的代数式分别表示出日销量增加后每天的销量和每台计算机的售价;
⑵写出y与x之间的函数关系式;
⑶用配方法将函数的解析式化为 的形式;
的形式;
⑷指出日销售额最大时每台计算机的售价应为多少?