摘要：A． S1<S2<S3 B． S2<S1<S3 C．S1<S3<S2 D．S1=S2=S3
网址：http://m.1010jiajiao.com/timu_id_745558[举报]
如图，点P为□ABCD的边CD上一点，若△PAB、△PCD和△PBC的面积分别为
s1、s2和s3，则它们之间的大小关系是( )
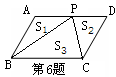
A. S3=S1+S2
B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
查看习题详情和答案>>
如下图，直线m和双曲线
交于A、B两点， P是线段AB上的点（不与A、B重台）．过点A、B、P分别向x轴作垂线，垂足分别 为C、D、E，连接OA、OB、OP.设△AOC的面积为S1，△BOD的面积为S2，△POE的面积为S3，则( )
A.Sl=S2=S3 B.S1>S2 >S3 c.S1=S2>S3 D.S1 =S2 <S3
查看习题详情和答案>>
如下图，直线m和双曲线
交于A、B两点， P是线段AB上的点（不与A、B重台）．过点A、B、P分别向x轴作垂线，垂足分别 为C、D、E，连接OA、OB、OP.设△AOC的面积为S1，△BOD的面积为S2，△POE的面积为S3，则( )
A.Sl=S2=S3 B.S1>S2 >S3 c.S1=S2>S3 D.S1 =S2 <S3
查看习题详情和答案>>
已知：直线a∥b，P、Q是直线a上的两点，M、N是直线b上的两点。
（1）如图1，线段PM、QN夹在平行直线a和b之间，四边形PMNQ为等腰梯形，其两腰PM=QN。请你参照图1，在图2中画出异于图1的一种图形，使夹在平行直线a和b之间的两条线段相等；
（2）我们继续探究，发现用两条平行直线a、b去截一些我们学过的图形，会有两条“曲线段相等”（曲线上两点和它们之间的部分叫做“曲线段”，把经过全等变换后能重合的两条曲线段叫做“曲线段相 等”。）
请你在图3中画出一种图形，使夹在平行直线a和b之间的两条曲线段相等。
（3）如图4，若梯形PMNQ是一块绿化地，梯形的上底PQ=m，下底MN=n，且m<n。现计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里，使得价格相同的花草不相邻。为了节省费用，园艺师应选择哪两块地种植价格较便宜的花草？请说明理由。
（1）如图1，线段PM、QN夹在平行直线a和b之间，四边形PMNQ为等腰梯形，其两腰PM=QN。请你参照图1，在图2中画出异于图1的一种图形，使夹在平行直线a和b之间的两条线段相等；
（2）我们继续探究，发现用两条平行直线a、b去截一些我们学过的图形，会有两条“曲线段相等”（曲线上两点和它们之间的部分叫做“曲线段”，把经过全等变换后能重合的两条曲线段叫做“曲线段相 等”。）
请你在图3中画出一种图形，使夹在平行直线a和b之间的两条曲线段相等。
（3）如图4，若梯形PMNQ是一块绿化地，梯形的上底PQ=m，下底MN=n，且m<n。现计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里，使得价格相同的花草不相邻。为了节省费用，园艺师应选择哪两块地种植价格较便宜的花草？请说明理由。
