2008年房山区中考模拟练习(一)
数学试卷
第Ⅰ卷 (共32分)
一、选择题(共8个小题,每小题4分,共32分)
1.4的相反数是
A、-4 B、
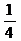 D、
D、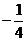
2.
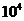 B. 37×
B. 37×
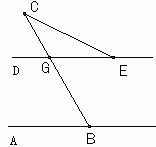
3、如图所示,直线DE∥AB,CB交DE于点G,若∠ABC=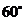 ,∠DEC=
,∠DEC=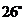 ,则∠C等于
,则∠C等于
A、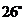 B、
B、 C、
C、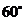 D、
D、
4、在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有
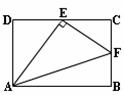
A、ΔADE∽ΔAEF B、 ΔECF∽ΔAEF
C、ΔAEF∽ΔABF D、 ΔADE∽ΔECF
5、2008年3月份,某市市区一周空气质量报告中二氧化氮指数的数据是:31 35 31 34 30 32 31,这组数据的中位数、平均数分别是
A.32,31
B. 31,
6、书架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是
A、 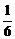 B、
B、 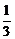 C、
C、 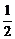 D、
D、 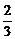
7、某中学团支部组织团员进行登山活动.他们开始以每小时a千米的速度登山,行进一段时间后队伍开始休息,由于前面山坡变陡,休息后他们以每小时b千米(0<b<a)的速度继续前进,直达山顶.在下列图象中,可以近似地刻画登山路程s(千米)随时间 t(时)变化的是
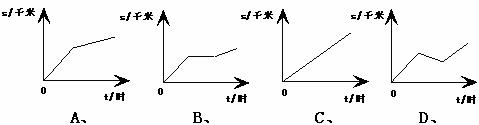
8、将下图所示的硬纸片围成正方体纸盒(接缝粘贴部分忽略不计),则围成的正方体纸盒是
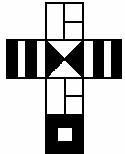
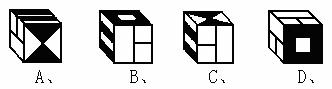
第Ⅱ卷 (共88分)
二、填空题(共4个小题,每小题4分,共16分)
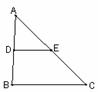
9、如图,在△ABC中,D、E分别是AB、AC边的中点,AB=4,AC=6,DE=2.4,则△ABC的周长是 .
10、若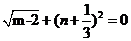 ,则
,则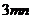 的值为
.
的值为
.
11、如果一个正方形的面积是10,那么它的边长的取值范围在整数 和 之间.
12、设正△ABC的边长为a,将△ABC绕它的中心(正△ABC外接圆的圆心)旋转60º得到对应的△A´B´C´,则A,B´两点间的距离等于______________.
三、解答题(共5个小题,共25分)
13.(本小题满分5分)
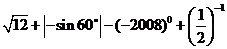
14.(本小题满分5分)
分解因式: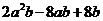
15.(本小题满分5分)
解不等式组: 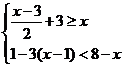
16.(本小题满分5分)
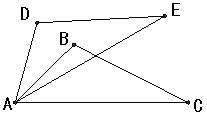
已知:如图,∠ABC=∠ADE,∠DAB=∠EAC,AB=AD.
求证:BC=DE.
17.(本小题满分5分)
化简求值: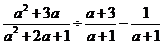 ,其中
,其中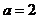 .
.
四、解答题(共2个小题,共10分)
18、(本小题满分5分)
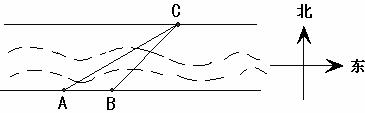
在一次数学活动课上,老师带领学生去测一条河的宽.如图所示,一学生在点A处观测到河对岸水边有一点C,测得C在北偏东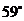 的方向上,沿河岸向东前行
的方向上,沿河岸向东前行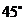 的方向上,
的方向上,
请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:
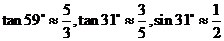 )
)
19.(本小题满分5分)
如图,△DEC内接于⊙O,AC经过圆心 交⊙O于点B,且AC⊥DE,垂足为
交⊙O于点B,且AC⊥DE,垂足为 ,连结AD、BE,若
,连结AD、BE,若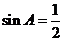 ,∠BED=30°.
,∠BED=30°.
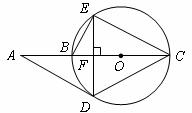
(1)求证:AD是⊙O的切线;
(2)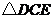 是否是等边三角形?请说明理由;
是否是等边三角形?请说明理由;
(3)若⊙O的半径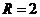 ,试求
,试求 的长.
的长.
五、解答题(本题满分5分)
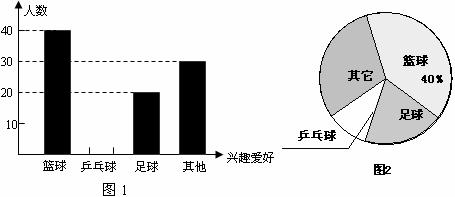
20.为响应国家要求中小学生每天锻练1小时的号召,某校准备开展“阳光体育运动”的活动.校学生会围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.绘制如下的统计图表:
各年级学生人数统计表
七年级
八年级
九年级
学生人数
240
360
(1)该校对多少名学生进行了抽样调查;
(2)请在图1中将“乒乓球”部分的图形补充完整;
(3)该校九年级学生比八年级学生多40人,请你计算该校九年级有学生多少人?并估计全校学生中最喜欢足球活动的人数约为多少?
六、解答题(共2个小题,共10分)
21.(本小题满分5分)
列方程或方程组解应用题:
某中学正在开展“微笑成长日记”佩带五色微笑圈的活动.小明调查了九年级(1)班佩带红色和蓝色微笑圈的人数情况,调查结果如下:
(1)佩带红色和蓝色微笑圈的共有24人;
(2)佩带蓝色微笑圈的人数比佩带红色微笑圈的人数的2倍少3人.请你根据以上情况帮助小明计算出该班佩带红色和蓝色微笑圈的各有多少人?
22.(本小题满分5分)
在平面直角坐标系xOy中,直线y=-2x沿x轴向右平移两个单位得到直线l,直线l与反比例函数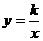 的图象的一个交点为A(a,8),试确定反比例函数的解析式.
的图象的一个交点为A(a,8),试确定反比例函数的解析式.
七、解答题(本题满分7分)
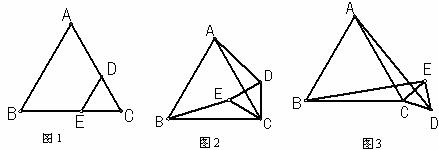
23.图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连结AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论.
(2)操作:若将图1中的△C′DE绕点C按顺时针方向任意旋转一个角度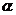 ,连结AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论.
,连结AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论.
(3)根据上面的操作过程,请你猜想当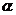 为多少度时,线段AD的长度最大?是多少?当
为多少度时,线段AD的长度最大?是多少?当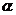 为多少度时,线段AD的长度最小?是多少?(不要求证明)
为多少度时,线段AD的长度最小?是多少?(不要求证明)
八、解答题(本题满分7分)
24、如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线l绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,设AC的长为t.
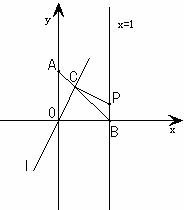
(1)当△AOC和△BCP全等时,求出t的值.
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论.
(3)设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.
九、解答题(本题满分8分)
25、已知:抛物线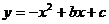 过点A(-1,0)、B(-2,-5),与y轴交于点C,顶点为D.
过点A(-1,0)、B(-2,-5),与y轴交于点C,顶点为D.
(1)求该抛物线的解析式;
(2)某直线过点A(-1,0),且与抛物线只有一个交点,求此直线的解析式;
(3)直线l过点C,且l∥x轴,E为l上一个动点,EF⊥x轴于F.求使DE+EF+BF的和为最小值的E、F两点的坐标,并直接写出DE+EF+BF的最小值.