2008-2009学年度滕州东南协作区第一学期九年级期中诊断性测评数学试卷
一、选择题(每题3分,共36分)下列各小题都给出了四个选项,其中只有一项是符合题目要求的。注意可以用各种不同的方法来解决你面前的选择题哦!
1.下列条件中不能判定两个三角形全等的是
A.三条边对应相等 B.有两条边和它们的夹角对应相等
C.两个角和一条边对应相等 D.两边和一个角对应相等
2.在△ABC中,AB=AC,如果一个内角为40°,那么∠B的度数为
A.40° B.70° C.40°或70° D.100°
3.若关于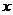 的一元二次方程
的一元二次方程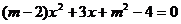 的常数项是0,则
的常数项是0,则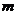 为
为
A.-2 B.+
4.如果关于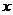 的一元二次方程
的一元二次方程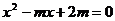 的一个根为1,那么方程的另一根为
的一个根为1,那么方程的另一根为
A.-1 B.-
5.下列各数中,可以用来证明命题“任何偶数都是8的整数倍”是假命题的反例是
A.32 B.
6.到△ABC的三个顶点距离相等的点是△ABC的
A.三条中线的交点 B.三条角平分线的交点
C.三条高线的交点 D.三条边的垂直平分线的交点
7.下列命题中错误的是
A.两条对角线相互平分的四边形是平行四边形
B.邻边相等的平行四边形是菱形
C.对角线相等的四边形是矩形
D.对角线相等的梯形是等腰梯形
8.下列命题中,其逆命题为真命题的是
A.直角都相等 B.面积相等的两个三角形全等
C.等边三角形是锐角三角形 D.若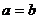 ,则
,则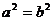
9.在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在的直线折叠,使点B恰好与点A重合。若CD=3,则AB的值为
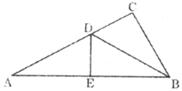
A. B.
B.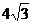 C.
C.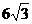 D.
D.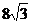
10.若顺次连接四边形各边中点所得到四边形是矩形,则原四边形一定是
A.等腰梯形 B.对角线相等且互相平分的四边形
C.平行四边形 D.对角线互相垂直的四边形
11.如下图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别是E、F。下列结论:
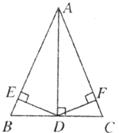
①DE=DF; ②BD=CD; ③AD上任意一点到AB、AC的距离相等;
④AD上任意一点到BC两端点的距离相等。其中正确结论的个数有
A.1个 B.2个 C.3个 D.4个
12.如下图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC,BD相交于O点,∠BCD=60°,则下列结论中:①梯形ABCD是轴对称图形;②AC平分∠DCB;③BC=2AB;④梯形ABCD是中心对称图形。其中不正确结论的个数有
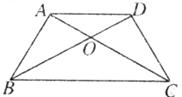
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共6小题,每小题4分,共24分)只要求在答题卷相应的位置上填写最后结果。开动你的脑筋,大家都在为你加油啊!
13.在△ABC中,∠C=90°,点D在斜边上,且AD=BD,CD=
14.三角形两边长分别为4和6,第三边是方程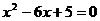 的解,则这个三角形的周长是__________。
的解,则这个三角形的周长是__________。
15.幸福药店的某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,该药店经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是_________。
16.将矩形纸片ABCD按如下图所示的方式折叠,得到菱形AECF。若AB=

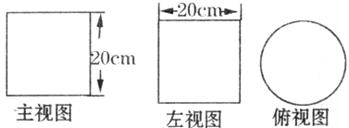
17.下图是一个包装盒的三视图,则这个包装盒的体积是_________(不求近似值)。
18.如下图所示,在△ABC中,分别以AB、AC、BC为边,在BC的同侧作等边△ABD,等边△ACE、等边△BCF。
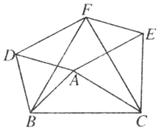
(1)四边形DAEF一定是_________;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足_________条件时,四边形DAEF是矩形;
②当△ABC满足_________条件时,四边形DAEF是菱形;
③当△ABC满足_________条件时,以D、A、E、F为顶点的四边形不存在。
三、解答题(19题10分,20题8分,21题7分,22题8分,23题7分,24题8分,25题12分,共计60分)解答要写出必要的文字说明、证明过程或演算步骤。如果你觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以,可不要有题目下面是空白的喔!
19.我们已经学习了一元二次方程的四种解法:因式分解法,开平方法,配方法和公式法。请从以下一元二次方程中任选两个,并选择你认为适当的方法分别解这两个方程(要求两题的解法不同)。
①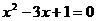 ②
②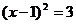 ③
③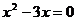 ④
④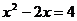
20.已知关于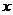 的一元二次方程
的一元二次方程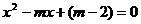 。
。
(1)判断此方程根的情况;
(2)设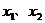 是关于已知方程的两个实数根,且
是关于已知方程的两个实数根,且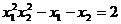 ,求
,求 的值。
的值。
21.某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其它生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.问应增加多少台机器,才可以使每天的生产总量达到30976件?
22.已知,如下图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,得到△DEF为等边三角形。
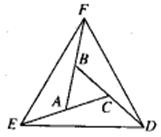
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形。
23.如图,在△ABC中,BC >AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF。
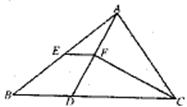
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为6,求△ABD的面积。
24.如下图,有一路灯杆OP,在灯光下,身高
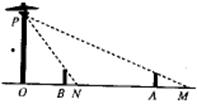
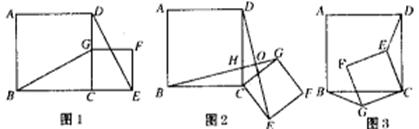
25.如下图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE我们探究下列图中线段BG、DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图2、如图3情形。请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断。
(2)将原题中正方形改为矩形(如下图4―6),且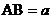 ,
, ,
,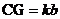
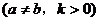 。第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由。
。第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由。
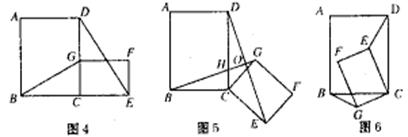
(3)在第(2)题图5中,连结DG、BE,且AB=3,BC=2,CE=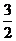 ,CG=1,求
,CG=1,求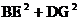 的值。
的值。