1．实验表明，人体内某种细胞的形状可近似地看作球形，它的直径约为0．00000156m，   则这个数用科学记数法表示是

A．0.156×10^―5m                      B．0.156×10⁵m

C．1.56×10^{―6 m}                       D．1.56×10⁶m

2．对分式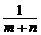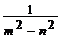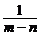，，通分，最简公分母为

A．(m+n)(m²-n²)                     B．(m²-n²)(m-n)

C．(m+n)²(m-n)                     D．m²-n²

3．某电视台举办的山东快书大赛上，六位评委给1号选手的评分如下：90，96，91，96，95，94．这组数据的中位数是

A．94.5                B．95                          C．96                          D．93.5

4．在坐标平面内，点P(4―2a，a―4)在第三象限内，则a的取值范围是

A．a＞2               B．a＜4                      C．2＜a＜4                 D．2≤a≤4

5．已知点A(-2,y₁)，B(-1，y₂)，C(3，y₃)都在反比例函数y=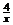的图像上，则

A．y_l<y₂<y₃       B．y₃<y₂<y₁               C．y₃<y_l<y₂        D．y₂<y_l<y₃

6．函数y=kx-l与y=-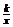在同一坐标系中的大致图像可能是

7．某市为了鼓励市民节约用水，按以下规定收取水费：①每户每月用水量不超过20m³，则每立方米水费l.2元；②每户每月用水量超过20m³，则超过部分每立方米水费2元．设某户一个月所交水费为y(元)，用水量xm³，则y与x的函数关系用图像表示为

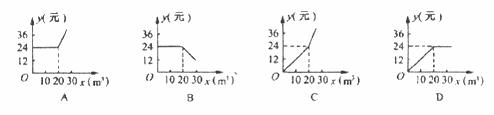
8．下列条件中,不能保证两个三角形全等的是

A．有两边和夹角对应相等               B．有两角和夹边对应相等

C．有两角和一边对应相等             D．等腰直角三角形

9．在四边形ABCD中，0是对角线的交点，能判定这个四边形为正方形的是

A．AC=BD，AB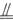CD                       B．AD∥BC，∠A=∠C

    C．AO=BO=CO=DO，AC⊥BD              D．AO=CO，BO=DO，AB=BC

10．C、D两点在线段AB的中垂线上，且∠ACB=50°，∠ADB=80°，则∠CAD为

A．15°         B．115°                  C．15°或115°   D．30°或13°

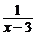11．若―2=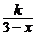有增根，则增根是_____，k=_____．

12．计算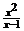―x的结果为_____．

13．若反比例函数y=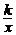的图像过(一4，0.5)，则k=_____，在图像所在每一象限内，y的值随x值的增大而_____。

14．已知直线经过点A(一3，一2)或点B(0，1)，则此直线的解析式是_____．

15．已知一次函数y=kx+4的图像与两坐标轴围成的三角形面积为6，则k=_____.

16．一支原长16cm的蜡烛被点燃后，其剩余长度 y (cm)与燃烧时间 x (分)成一次函数关系．若燃烧5分钟后，其剩余长度为l4cm，则y与x的函数关系式为_____。这支蜡烛最多可燃烧_____分钟．

17．甲、乙两名战士用步枪射击，各打l0发，所中环数如下；

        甲：7  8  6  8  6  5  9  10  7  4

        乙：9  5  7  8  7  6  8  6   7  7

        那么S²_甲=_____，S²_乙=_____，_____的射击情况较稳定．

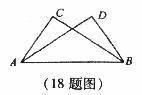
18．如图，已知∠ACB=∠BDA=90°，要使△ACB≌△BDA，还需要添加的条件是_____．(添一个符合要求的条件即可)

19．命题“等腰三角形的两个底角相等”的逆命题是____________________.

20．点A，B，C，D在同一平面内，从①AB∥CD；②AB=CD；③BC∥AD；④BC=AD这四个条件中任意选两个，不能使四边形ABCD是平行四边形的选法是_____.

21．计算：（―）÷.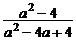

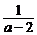22．解方程：+=.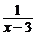

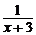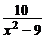23．甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路驶向C城．已知A、C两城的距离为450千米，B、C两城的距离为400千米，甲车比乙车的速度快l0千米／时，结果两辆车同时到达C城，求两车的速度．

24．如下图所示，已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=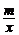(m≠0)的图象在第一象限交于C点，CD垂直于x轴，垂足为D．若OA=OB=OD=1

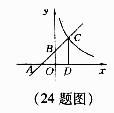
(1)求点A、B、D的坐标；

(2)求一次函数和反比例函数关系式．

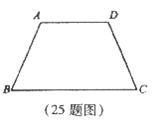
25．如下图，在梯形ABCD中，AD∥BC，AB=CD．

    (1)利用尺规作AD的中点E(保留作图痕迹，不写作法和证明)．

    (2)连结EB、EC．

    求证：∠ABE=∠DCE

26．某校要从小王和小李两名同学中选拔一个人参加全国数学竞赛，在最近的五次选拔测试中，他俩的成绩如下表：

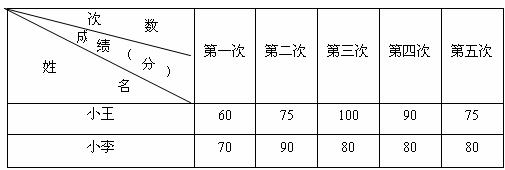
根据上表解答下列问题：

(1)完成下表：

(2)在这五次测试中，成绩比较稳定的是谁?若将80分以上(含80分)的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少?

(3)历届比赛表明，成绩达到80分以上(含80分)就很可能获奖，成绩达到90分以上(含90分)就很可能获得一等奖，那么你认为应选谁参加比赛比较合适?说明你的理由．