2008年福州市初中毕业会考、高级中等学校招生考试
数学试卷
(全卷共4页,三大题,共22小题;满分150分;考试时间120分钟)
友情提示:所有答案都必须填涂在答题卡上,答在本试卷上无效。
一、选择题(共10小题,每小题4分,满分40分;每小题只有一个正确的选项,请在答题卡的相应位置填涂)
1.-5的相反数是
A.5 B.-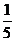 D.
D.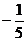
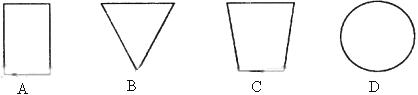
2.如图所示的物体是一个几何体,其主视图是

3.2008北京奥运会主会场“鸟巢”的座席数是91000个,这个数用科举记数法表示为
A.0.91×105 B.9.1×
4.实数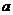 、
、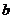 在数轴上的位置如图所示,下列各式正确的是
在数轴上的位置如图所示,下列各式正确的是

A. B.
B. C.
C. D.
D.
5.下列计算正确的是
A. B.
B.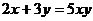
C. D.
D.
6.下列调查中,适合用全面调查方式的是
A.了解某班学生“
C.了解一批炮弹的杀伤半径 D.了解一批袋装食品是否含有防腐剂
7.已知三角形的两边长分别为
A.
8.一次函数 的图象大致是
的图象大致是

9.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100º,则∠BOD的度数是
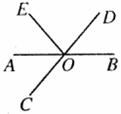
A.20º B.40º C.50º D.80º
0.已知抛物线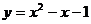 与
与 轴的一个交点为(
轴的一个交点为( ,0),则代数式
,0),则代数式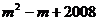 的值为
的值为
A.2006 B.
二、填空题(共5小题。每小题4分,满分20分。请将答案填入答题卡的相应位置)
11.因式分解: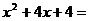 。
。
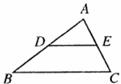
12.如图,在△ABC中,D、E分别是AB、AC的中点,若DE=5,则BC的长是 。
13.在一个袋子中装有除颜色外其它均相同的2个红球和3个白球,从中任意摸出一个球,则摸到红球的概率是 。
14.如图,AB是⊙O的弦,OC⊥AB于点C,若AB=
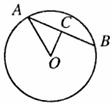
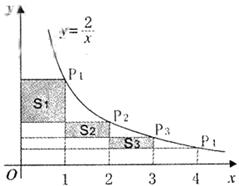
15.如图,在反比例函数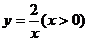 的图像上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作
的图像上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作 轴与
轴与 轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=
。
轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=
。
三、解答题(满分90分。请将解答过程填入答题卡的相应位置,作图或添辅助线用铅笔画完,需用水笔再描黑)
16.(每小题7分,满分14分)
(1)计算:
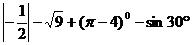 ;
;
(2)化简: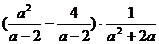 。
。
17.(每小题7分,满分14分)
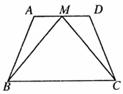
(1)如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,求证:MB=MC。
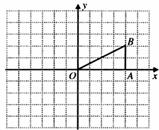
(2)如图,在Rt△OAB中,∠OAB=90º,且点B的坐标为(4,2)。
①画出△OAB向下平移3个单位后的△O
②画出△OAB绕点O逆时针旋转90º后的△OA2B2,并求点A旋转到点A2所经过的路线长(结果保留 )。
)。
18.(本题满分12分)
某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下两幅统计图,请你结合图中所给信息解答下列问题:
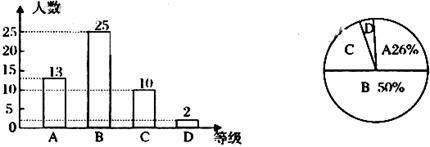
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图中C级所在的扇形圆心角度数;
(3)该班学生体育测试成绩的中位数落在哪个等级内;
(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
19.(本题满分11分)
如图,AB是⊙O的直径,AD是弦,∠DAB=22.5º,延长AB到点C,使得∠ACD=45º。
(1)求证:CD是⊙O的切线;
(2)若AB= ,求BC的长。
,求BC的长。

20.(本题满分12分)
今年5月12日,四川汶川发生了里氏8.0级大地震,给当地人民造成了巨大的损失。“一方有难,八方支援”,我市锦华中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:
班级
(1)班
(2)班
(3)班
金额(元)
2000

信息一:这三个班的捐款总金额是7700元;
信息二:(2)班的捐款金额比(3)班的捐款金额多300元;
信息三:(1)班学生平均每人捐款的金额大于48元,小于51元。
请根据以上信息,帮助
(1)求出(2)班与(3)班的捐款金额各是多少元;
(2)求出(1)班的学生人数。
21.(本题满分13分)
如图,已知△ABC是边长为
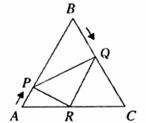
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ?
22.(本题满分14分)
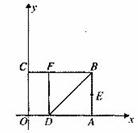
如图,以矩形OABC的顶点O为原点,OA所在的直线为 轴,OC所在的直线为
轴,OC所在的直线为 轴,建立平面直角坐标系。已知OA=3,OC=2,点E是AB的中点.在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处。
轴,建立平面直角坐标系。已知OA=3,OC=2,点E是AB的中点.在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处。
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交 轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在 轴、
轴、 轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由。
轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由。