摘要：(1)当t=2时.判断△BPQ的形状.并说明理由,(2)设△BPQ的面积为S(cm2).求S与t的函数关系式,(3)作QR∥BA交AC于点R.连接PR.当t为何值时.△APR∽△PRQ?
网址：http://m.1010jiajiao.com/timu_id_725438[举报]
已知点A（0，2）、B（2
，2）、C（0，4）．
（1）如图1，连接BO、BC、AB．
①填空：AC的长为
②试判断△OBC的形状，并说明理由；
（2）如图2，过点C向右作平行于x轴的射线，点P是射线上的动点，连接BP，以BP为一边在△ABP外侧作等边△BPQ，当四边形ABQP为梯形时，求点P的横坐标．
查看习题详情和答案>>
| 3 |
（1）如图1，连接BO、BC、AB．
①填空：AC的长为
2
2
，AB的长为2
| 3 |
2
；| 3 |
②试判断△OBC的形状，并说明理由；
（2）如图2，过点C向右作平行于x轴的射线，点P是射线上的动点，连接BP，以BP为一边在△ABP外侧作等边△BPQ，当四边形ABQP为梯形时，求点P的横坐标．
如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：
（1）当t＝2时，判断△BPQ的形状，并说明理由；
（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；
（3）作QR//BA交AC于点R，连结PR，当t为何值时，△APR∽△PRQ？
如图，已知△ABC是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB、BC方向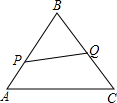
匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．
（1）出发后运动2s时，试判断△BPQ的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；
（2）设运动时间为t，△BPQ的面积为S，请用t的表达式表示S． 查看习题详情和答案>>
匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．（1）出发后运动2s时，试判断△BPQ的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；
（2）设运动时间为t，△BPQ的面积为S，请用t的表达式表示S． 查看习题详情和答案>>
匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．