2008年贵阳市中考模拟试卷八
数学
一、选择题(以下每小题都有A、B、C、D四个选项。其中只有一个选项正确。请把正确选项的字母选入该题的括号内。每小题4分。共20分)
1.计算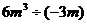 的结果是( ).
的结果是( ).
A.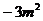 B.
B.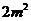 C.
C.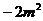 D.
D.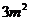
2.据2006年末统计显示,免除农村义务教育阶段学杂费的西部地区和部分中部地区的 学生约52000000名,这个学生人数用科学记数法表示正确的是( ).
A.5.2×106 B.52×106 C.5.2×107 D.0.52×108
3.甲、乙两名学生进行射击练习,两人在相同条件下各射击5次,射击成绩统计如下:
命中环数(单位:环)
7
8
9
10
甲命中相应环数的次数
2
2
0
1
甲命中相应环数的次数
1
3
1
0
从射击成绩的平均数评价甲、乙两人的射击水平,则( ).
A.甲比乙高 B.甲、乙一样 C.乙比甲高 D.不能确定
4.如下图,用放大镜将图形放大,应该属于( ).

A.相似变换 B.平移变换 C.对称变换 D.旋转变换
5.已知二次函数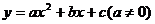 的图像如下图所示,有下列5个结论:
的图像如下图所示,有下列5个结论:
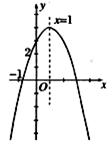
(1)abc>0;(2)b<a+c;(3)4a+2b+c>0;(4)2c<3b;(5)a+b>m(am+b)(m≠1的实数)其中正确的结论有( ).
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共30分)
6.请写出一对互为相反数的数: 和 .
7.分解因式: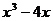 =
.
=
.
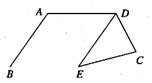
8.如下图,已知,线段DE由线段AB平移而得,AB=DC=4cm,EC=5cm,则△DCE的周长是 cm.
9.如下图,A、B、C是⊙O上三点.∠ACB=40°,则∠ABO= 度.

10.掷一枚质地均匀的小正方体,它的六个面上分别标有数字1,2,3,4,5,6,则朝上一面的数字是质数的概率是 .
11.在△ABC中,若AB=8,BC=6,则第三边AC的长度m的取值范围是 .
12.如下图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.

13.某班主任老师想了解本班学生平均每月有多少零用钱,随机抽取了10名同学进行调查,他们每月的零用钱数目是(单位:元)10,20,20,30,20,30,10,10,50,100,则这组数据的中位数是 元.
14.如下图,已知函数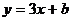 和
和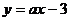 的图像交于点P(一2,一3),则根据图像可得不等式
的图像交于点P(一2,一3),则根据图像可得不等式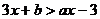 的解集是
.
的解集是
.
15.如下图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=5cm,BD=12cm,则梯形ABCD的高是 cm。
三、解答题
16.(本题7分)
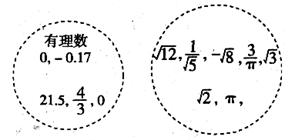
在下面两个集合中各有一些实数,请你分别从中选出2个有理数和2个无理数,再用“+,―,×,÷”中的3种符号将选出的4个数进行3次运算,使得运算的结果是一个正整数.

图书种类
频数
频率
科普常识
840
B
名人传记
816
0.34
漫画丛书
A
0.25
其他
144
0.06
18.(本题10分)
“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%.该专业户去年实际生产小麦、玉米各多少吨?
19.(本题10分)
如下图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?

20.(本题10分)
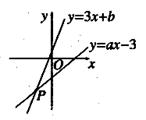
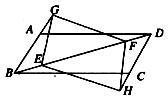
如下图,已知在平行四边形ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:四边形GEHF是平行四边形.
21.(本题9分)
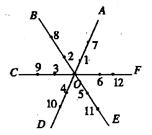
如下图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)“17”在射线 上;(3分)
(2)请任意写出三条射线上数字的排列规律;(3分)
(3)“2007”在哪条射线上?为什么?(3分)
22.(本题10分)
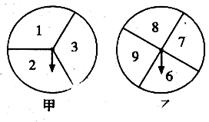
如下图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:
同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
(1)请你通过画树状图的方法求小颖获胜的概率.
(2)你认为该游戏规则是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.
23.(本题13分)
我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满根据下表提供的信息,解答以下问题:
脐 橙 品 种
A
B
C
每辆汽车运载量(吨)
6
5
4
每吨脐橙获得(百元)
12
16
10
(1)设装运A种脐橙的车辆数为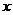 ,装运B种脐橙的车辆数为y,求y与
,装运B种脐橙的车辆数为y,求y与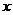 之间的函数关系式;(3分)
之间的函数关系式;(3分)
(2)如果装运每种脐橙的车辆数都不少于4吨,那么车辆的安排有几种?并写出每种安排方案.(6分)
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.(4分)
24.(本题9分)
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):
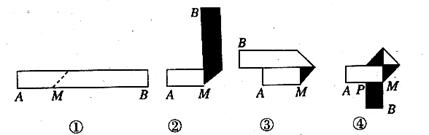
如果由信纸折成的长方形纸条(图①)长为26cm,宽为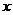 cm,分别回答下列问题:
cm,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求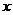 的取值范围。(4分)
的取值范围。(4分)
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用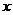 表示).(5分)
表示).(5分)
25.(本题12分)
东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
卖出价格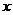 (元/件)
(元/件)
50
51
52
53
…
销售量P(件)
500
490
480
470
…
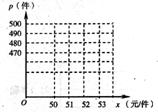
(1)以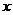 作为点的横坐标,P作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连接各点所得的图形,判断P与
作为点的横坐标,P作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连接各点所得的图形,判断P与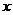 的函数关系式;(6分)
的函数关系式;(6分)
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格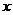 (元/件)的函数关系式.
(元/件)的函数关系式.
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?(6分)