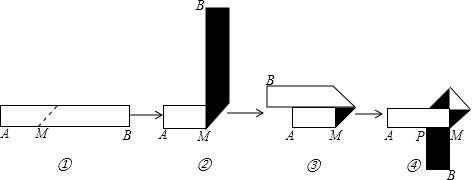
摘要:(1)为了保证能折成图④的形状.试求的取值范围.
网址:http://m.1010jiajiao.com/timu_id_695177[举报]
生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程是这样的(阴影部分表示纸条反面):
(l)如果信纸折成的长方形纸条宽为2cm, 为了保证能折成图丁形状(即纸条两端均超出点P),纸条长至少多少厘米?纸条长最小时.长方形纸条面积是多少?
(2)假设折成图丁形状纸条宽 xcm, 并且一端超出P点 2cm,另一端超出P点3cm,若信纸折成的长方形纸条长为ycm.求y关于x的函数关系式,用含x的代数式表示折成的图丁所示的平面图形的面积S;
(3)若希望(2)中纸条两端超出P点长度相等,即最终图形丁是轴对称图形,如果
y = 15cm ,则开始折叠时点M应放在什么位置?
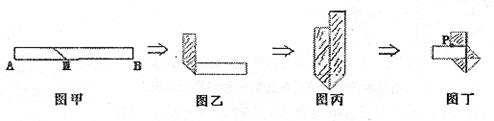
生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程是这样的(阴影部分表示纸条反面):
(1)如果信纸折成的长方形纸条宽为2cm,为了保证能折成图丁形状(即纸条两端均超出点P),纸条长至少多少厘米?纸条长最小时.长方形纸条面积是多少?
(2)假设折成图丁形状纸条宽xcm,并且一端超出P点2cm,另一端超出P点3cm,若信纸折成的长方形纸条长为ycm.求y关于x的函数关系式,用含x的代数式表示折成的图丁所示的平面图形的面积S;
(3)若希望(2)中纸条两端超出P点长度相等,即最终图形丁是轴对称图形,如果y=15cm,则开始折叠时点M应放在什么位置?
 查看习题详情和答案>>
查看习题详情和答案>>
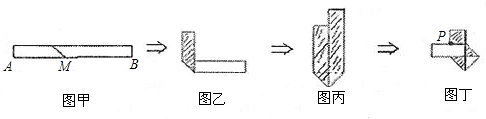
(1)如果信纸折成的长方形纸条宽为2cm,为了保证能折成图丁形状(即纸条两端均超出点P),纸条长至少多少厘米?纸条长最小时.长方形纸条面积是多少?
(2)假设折成图丁形状纸条宽xcm,并且一端超出P点2cm,另一端超出P点3cm,若信纸折成的长方形纸条长为ycm.求y关于x的函数关系式,用含x的代数式表示折成的图丁所示的平面图形的面积S;
(3)若希望(2)中纸条两端超出P点长度相等,即最终图形丁是轴对称图形,如果y=15cm,则开始折叠时点M应放在什么位置?
 查看习题详情和答案>>
查看习题详情和答案>>
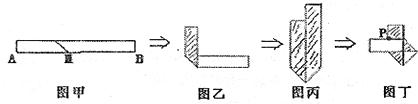
24、生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程是这样的(阴影部分表示纸条反面):
(l)如果信纸折成的长方形纸条宽为4cm,为了保证能折成图丁形状(即纸条两端均刚好到达点P),纸条长至少多少厘米?纸条长最小时.长方形纸条面积是多少?
(2)假设折成图丁形状纸条宽xcm,并且一端超出P点2cm,另一端超出P点3cm,
①请用x的代数式表示信纸折成的长方形纸条长.
②用含x的代数式表示折成的图丁所示的平面图形的面积S.
查看习题详情和答案>>
(l)如果信纸折成的长方形纸条宽为4cm,为了保证能折成图丁形状(即纸条两端均刚好到达点P),纸条长至少多少厘米?纸条长最小时.长方形纸条面积是多少?
(2)假设折成图丁形状纸条宽xcm,并且一端超出P点2cm,另一端超出P点3cm,
①请用x的代数式表示信纸折成的长方形纸条长.
②用含x的代数式表示折成的图丁所示的平面图形的面积S.