2008年乐陵市第二次练兵模拟试题
数学试题(人教版)
(时间:120分钟;满分:120分)
第 I 卷(选择题,共24分)
一、选择题:(本大题共8小题,每小题3分,共24分,在每小题给出的四个选项中有一项是正确的, 请把正确的选项选出来,每小题选对得3分, 选错、不选或选出的答案超过一个均记零分)
1、绝对值为4的实数是( )
A.-4 B.
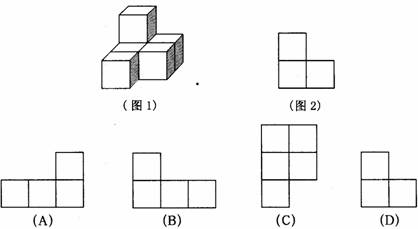
2、由几个小立方体搭成的一个几何体如图1所示,它的主(正)视图见图2,那么它的右视图为( )
3、如图,方格纸上一圆经过(2 , 5)、(2 , -3)两点,且此两点为圆与方格纸横线的切点,则该圆圆心的坐标为( )
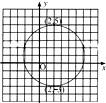
A.(1, 1) B.(2, 2) C.(2, 1) D.(3, 1)
4、下列图中是太阳光下形成的影子是( )。
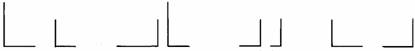
A. B. C. D
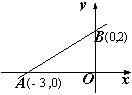
5、如图,一次函数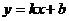 的图像经过A、B两点,则
的图像经过A、B两点,则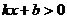 解集是( )
解集是( )
A.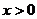 B.
B.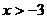 C.
C.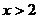 D.
D.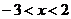
6、如图,现有一圆心角为90°,半径为
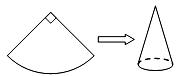
A.
7、已知函数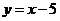 ,令x =
,令x =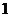 ,
,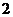 ,
,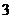 ,
,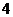 ,
,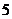 ,可得函数图象上的5个点.在这5个点中随机取两个点
,可得函数图象上的5个点.在这5个点中随机取两个点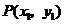 ,
,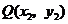 ,则
,则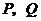 两点在同一反比例函数图象上的概率是( )
两点在同一反比例函数图象上的概率是( )
A.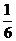 B.
B.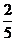 C.
C.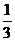 D.
D.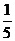
8、2008年第29届奥运会即将在北京举行,某厂经授权生产的奥运纪念品深受人们欢迎,今年2月份以来,该产品在原有库存量为m(m>0)的情况下,日销量与产量持平,4月底以来需求量增加,在生产能力不变的情况下,该产品一度脱销。下图能大致表示今年2月份以来库存量y与时间t之间函数关系的是 ( )
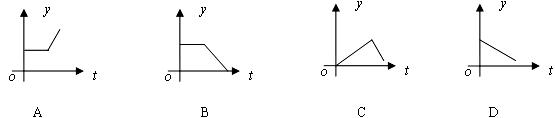
第 II 卷(非选择题,共96分)
二、填空题:(本大题共8小题,计24分,只要求填写最后结果,每小题填对得3分)
9、继短信之后,音乐类产品逐步成为我国手机用户的最爱和移动通信新的增长点。目前,中国移动彩铃用户数已超过40 000 000,用科学记数法可表示为:
10、关于x的不等式x

11、老师给出一个函数,甲、乙各指出了这个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,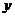 随
随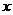 的增大而减小.
的增大而减小.
请你写一个满足上述性质的函数表达式 .
12、如图,直线L是一条河,P、Q两地相距10千米,P、Q两地到L的距离分别为

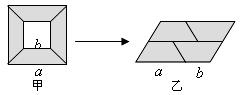
13、如图,从边长为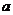 的大正方形纸板中挖去一个边长为
的大正方形纸板中挖去一个边长为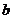 的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算阴影部分的面积可以验证公式______________.
的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算阴影部分的面积可以验证公式______________.
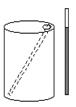
14、如图,一油桶高
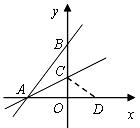
15、如图,直线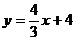 与x轴,
与x轴,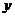 轴分别交于A,B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在
轴分别交于A,B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在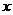 轴上的点D处,则点C的坐标是_________________.
轴上的点D处,则点C的坐标是_________________.
16、小明家离学校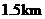 ,小明步行上学需
,小明步行上学需 ,那么小明步行速度
,那么小明步行速度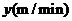 可以表示为
可以表示为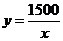 ;水平地面上重
;水平地面上重 的物体,与地面的接触面积为
的物体,与地面的接触面积为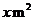 ,那么该物体对地面压强
,那么该物体对地面压强 可以表示为
可以表示为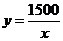 ;
; ,函数关系式
,函数关系式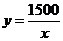 还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
三、解答题:(本大题8小题,计72分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本题满分6分)
用图象法解方程组 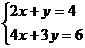
18.(本题满分8分)
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?说明理由。

求证:S四边形ABCD=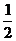 AC?BD.
AC?BD.
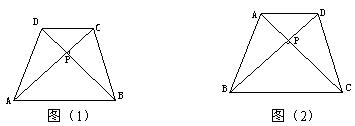
证明:∵AC⊥BD,∴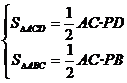
∴S四边形ABCD=S△ACD+ S△ABC=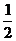 AC?PD+
AC?PD+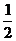 AC?PB=
AC?PB=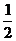 AC(PD+PB)=
AC(PD+PB)=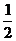 AC?BD。
AC?BD。
解答问题:
(1)上述证明得到的性质可叙述为: .
(2)已知:如图(2),等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=
20.(本题满分9分)
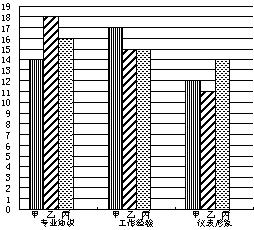
某集团公司对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).
(1)利用图中提供的信息,在专业知识方面3人得分的极差是多少?在仪表形象方面谁最有优势?
(2)如果专业知识、工作经验、仪表形象三个方面的重要性之比为10∶7∶3,那么作为人事主管,你应该录用哪一位应聘者?为什么?
21.(本题满分10分)
如图,AB是⊙O的弦,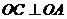 交AB于点C,过点B的直线交OC的延长线于点E,当
交AB于点C,过点B的直线交OC的延长线于点E,当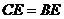 时,直线BE与⊙O有怎样的位置关系?并证明你的结论.
时,直线BE与⊙O有怎样的位置关系?并证明你的结论.

22.(本题满分10分)
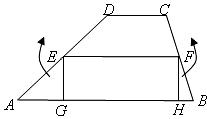
如图 ,梯形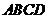 中,
中,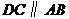 ,
,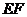 是中位线,
是中位线,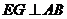 于
于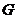 ,
, 于
于 ,梯形的高
,梯形的高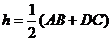 .沿着
.沿着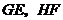 分别把
分别把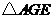 ,
, 剪开,然后按图中箭头所指方向,分别绕着点
剪开,然后按图中箭头所指方向,分别绕着点 旋转
旋转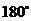 ,将会得到一个什么样的四边形?简述理由.
,将会得到一个什么样的四边形?简述理由.
23.(本题满分10分)
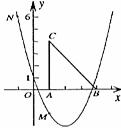
如图,二次函数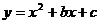 的图象经过点M(1,―2)、N(―1,6)。
的图象经过点M(1,―2)、N(―1,6)。
(1)求二次函数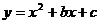 的关系式。
的关系式。
(2)把Rt△ABC放在坐标系内,其中∠CAB = 90°,点A、B的坐标分别为(1,0)、(4,0),BC = 5。将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离。
24.(本题满分10分)
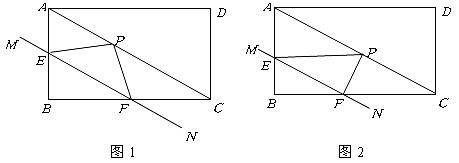
已知四边形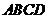 是矩形,
是矩形,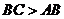 ,直线
,直线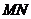 分别与
分别与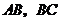 交与
交与 两点,
两点,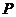 为对角线
为对角线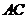 上一动点(
上一动点(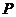 不与
不与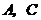 重合).
重合).
(1)当点 分别为
分别为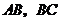 的中点时,(如图1)问点
的中点时,(如图1)问点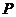 在
在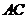 上运动时,点
上运动时,点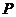 、
、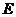 、
、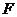 能否构成直角三角形?若能,共有几个,并在图1中画出所有满足条件的三角形.
能否构成直角三角形?若能,共有几个,并在图1中画出所有满足条件的三角形.
(2)若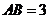 ,
, ,
,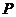 为
为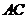 的中点,当直线
的中点,当直线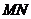 移动时,始终保持
移动时,始终保持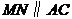 ,(如图2)求
,(如图2)求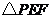 的面积
的面积 与
与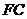 的长
的长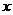 之间的函数关系式.
之间的函数关系式.