摘要：(1)当点分别为的中点时.问点在上运动时.点..能否构成直角三角形?若能.共有几个.并在图1中画出所有满足条件的三角形．
网址：http://m.1010jiajiao.com/timu_id_695035[举报]
22、如图所示，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1m/s，点Q运动的速度是2m/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t s，解答下列问题：（1）当点Q到达点C时，PQ与AB的位置关系如何？请说明理由．
（2）在点P与点Q的运动过程中，△BPQ是否能成为等边三角形？若能，请求出t，若不能，请说明理由．
如图，梯形ABCD中，AD∥BC，∠BAD=90°，CE⊥AD于点E，AD=8cm，BC=4cm，AB=5cm．从初始时刻开始，动点P，Q 分别从点A，B同时出发，运动速度均为1cm/s，动点P沿A-B--C--E的方向运动，到点E停止；动点Q沿B--C--E--D的方向运动，到点D停止，设运动时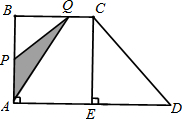
间为xs，△PAQ的面积为ycm2，（这里规定：线段是面积为0的三角形）
解答下列问题：
（1）当x=2s时，y= cm2；当x=
s时，y= cm2．
（2）当5≤x≤14 时，求y与x之间的函数关系式．
（3）当动点P在线段BC上运动时，求出y=
S梯形ABCD时x的值．
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值． 查看习题详情和答案>>
间为xs，△PAQ的面积为ycm2，（这里规定：线段是面积为0的三角形）解答下列问题：
（1）当x=2s时，y=
| 9 |
| 2 |
（2）当5≤x≤14 时，求y与x之间的函数关系式．
（3）当动点P在线段BC上运动时，求出y=
| 4 |
| 15 |
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值． 查看习题详情和答案>>
如图，在平行四边形ABCD中，AB在x轴上，D点y轴上，∠C=60°，BC=6，B点坐标为（4，0）．点M是边AD上一点，且DM：AD=1：3．点E、F分别从A、C同时出发，以1厘米/秒的速度分别沿AB、CB向点B运动（当点F运动到点B时，点E随之停止运动），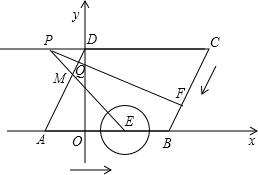
EM、CD的延长线交于点P，FP交AD于点Q．⊙E半径为
，设运动时间为x秒．
（1）求直线BC的解析式；
（2）当x为何值时，PF⊥AD；
（3）在（2）问条件下，⊙E与直线PF是否相切？如果相切，加以证明，并求出切点的坐标；如果不相切，说明理由． 查看习题详情和答案>>
EM、CD的延长线交于点P，FP交AD于点Q．⊙E半径为| 5 | 2 |
（1）求直线BC的解析式；
（2）当x为何值时，PF⊥AD；
（3）在（2）问条件下，⊙E与直线PF是否相切？如果相切，加以证明，并求出切点的坐标；如果不相切，说明理由． 查看习题详情和答案>>
如图①，在平面直角坐标系xoy中，直线y=-
x+2分别交x轴、y轴于C、A两点．将射线AM绕着点A顺时针旋45°得到射线AN．点D为AM上的动点，点B为AN上的动点，点C在∠MAN的内部．
（1）求线段AC的长；
（2）当AM∥x轴，且四边形ABCD为梯形时，求△BCD的面积；
（3）求△BCD周长的最小值；
（4）当△BCD的周长取得最小值，且BD=
时，△BCD的面积为 ．（第（4）问需填写结论，不要求书写）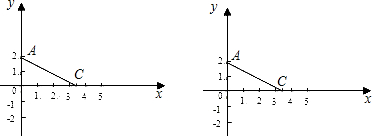
查看习题详情和答案>>
| ||
| 3 |
（1）求线段AC的长；
（2）当AM∥x轴，且四边形ABCD为梯形时，求△BCD的面积；
（3）求△BCD周长的最小值；
（4）当△BCD的周长取得最小值，且BD=
5
| ||
| 6 |
查看习题详情和答案>>
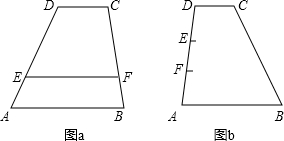
如图a，梯形ABCD中，AB∥CD，AB=a，CD=b，点E、F分别是两腰AD、BC上的点，且EF∥AB，设EF到CD、AB的距离分别为d1、d2，某同学在对这一图形进行研究时，发现如下事实：
①当
=
时，有EF=
；
当
=
时，有EF=
；
当
=
时，有EF=
；
当
=
时，有EF=
；
②当
=
时，有EF=
；当
=
时，有EF=
；
当
=
时，有EF=
；当
=
时，有EF=
．
根据以上结论，解答下列问题：
（1）猜想当
=
和
=
时，分别能得到什么结论（其中m、n均为正整数）？
（2）进一步猜想当
=
时，有何结论（其中m、n均为正整数）？并证明你的结论；
（3）如图b，有一块梯形耕地ABCD，AB∥CD，CD=100米，AB=300米，AD=500米，在AD上取两点E、F，使DE=200米，EF=150米，分别从E、F两处为起点开挖两条平行于两底的水渠，直到另一腰，求这两条水渠的总长度．
查看习题详情和答案>>
①当
| d1 |
| d2 |
| 1 |
| 1 |
| a+b |
| 2 |
当
| d1 |
| d2 |
| 1 |
| 2 |
| a+2b |
| 3 |
当
| d1 |
| d2 |
| 1 |
| 3 |
| a+3b |
| 4 |
当
| d1 |
| d2 |
| 1 |
| 4 |
| a+4b |
| 5 |
②当
| d1 |
| d2 |
| 2 |
| 1 |
| 2a+b |
| 3 |
| d1 |
| d2 |
| 3 |
| 1 |
| 3a+b |
| 4 |
当
| d1 |
| d2 |
| 4 |
| 1 |
| 4a+b |
| 5 |
| d1 |
| d2 |
| 5 |
| 1 |
| 5a+b |
| 6 |
根据以上结论，解答下列问题：
（1）猜想当
| d1 |
| d2 |
| 1 |
| n |
| d1 |
| d2 |
| m |
| 1 |
（2）进一步猜想当
| d1 |
| d2 |
| m |
| n |
（3）如图b，有一块梯形耕地ABCD，AB∥CD，CD=100米，AB=300米，AD=500米，在AD上取两点E、F，使DE=200米，EF=150米，分别从E、F两处为起点开挖两条平行于两底的水渠，直到另一腰，求这两条水渠的总长度．
查看习题详情和答案>>