2008年滨州市滨城区九年级第一次模拟考试数学试题
注意事项:
1.答题前请考生务必在试卷的规定位置将自己的学校、姓名、考试号等内容填写准确.
2.本试题分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题,共42分,第Ⅱ卷为非选择题,共78分,全卷共120分,考试时间为120分钟.考试不允许使用计算器.
第Ⅰ卷(选择题 共42分)
一、选择题:本题共12小题,共42分.在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在第Ⅱ卷相应的表格内,第1-6小题每小题3分,第7-12小题每小题4分,错选、不选、多选均不得分.
1. 比较数的大小,下列结论错误的是:
(A)-5<-3 (B)2>-3>0 (C)- <0<
<0<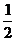 (D)-
(D)- >-
>- >-
>-
2. 纳米是一种长度单位,1纳米= 米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示该种花粉的直径为 :
米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示该种花粉的直径为 :
(A) 米
米 米 (C)3.5
米 (C)3.5 米 (D)3.5
米 (D)3.5 米
米
3. 若规定误差小于1,那么 的估算值为:
的估算值为:
(A)3 (B)7或8 (C)8 (D)6或7
4. 下列根式中是最简二次根式的是:
(A) (B)
(B) (C)
(C) (D)
(D)
5. 下列平面图形中不能围成正方体的是:

6. 一只袋中有红球m个,白球7个,黑球n个,每个球除颜色外都相同,从中任取一个,取得白球的可能性与不是白球的可能性相同,那么m与n的关系是:
(A) (B)
(B) (C)
(C) (D)
(D)
7. 如图, ,
, ,那么
,那么 与
与 之间的关系正确的是:
之间的关系正确的是:

(A) (B)
(B)
(C) (D)
(D)
8. 当你乘车沿一条平坦的大道向前行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于它们前面那些矮一些的建筑物后面去了,这是因为:
(A)汽车开的很快 (B)盲区减小 (C)盲区增大 (D)无法确定
9. 已知二次函数y=2x2+9x+34,当自变量x取两个不同的值x1、x2时,函数值相等,则当自变量x取x1+x2 时的函数值与:
(A)x=1 时的函数值相等 (B)x=0时的函数值相等
(C)x= 时的函数值相等 (D)x=-
时的函数值相等 (D)x=- 时的函数值相等
时的函数值相等
10. 下图中表示一次函数 与正比例函数
与正比例函数 (
( ,
, 是常数,且
是常数,且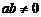 )图象的是
.
)图象的是
.
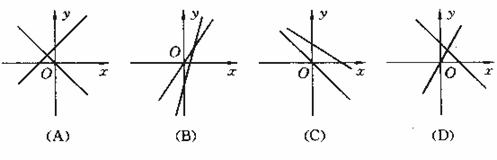
11. 下面是李刚同学在一次测验中解答的填空题,其中答对的是:
(A)若 ,则
,则 ;
;
(B)方程 的解为
的解为 ;
;
(C)若分式 的值为零,则
的值为零,则 ;
;
(D)用公式法解方程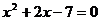 的结果是
的结果是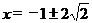 .
.
12. 方程组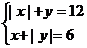 解的组数为:
解的组数为:
(A)1 (B)2 (C)3 (D)4
第Ⅱ卷 非选择题部分(共78分)
二、填空题:本题共5小题,共20分.只要求填写最后结果,每小题填对得4分.
13. 直线l上的一点到圆心的距离等于⊙O的半径,则l与⊙O的位置关系是 .
14. 在平行四边形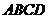 中,
中,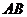 、
、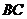 、
、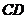 的长度分别为
的长度分别为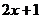 、
、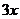 、
、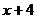 ,则平行四边形
,则平行四边形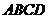 的周长是_____________.
的周长是_____________.
15. 在直角坐标系中,已知点A(4,y)、B(x,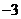 ), 若AB//x轴,且线段AB的长为5,则xy=
.
), 若AB//x轴,且线段AB的长为5,则xy=
.
16. 观察下列各式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52;……,请写出第n个式子 .
17. 小敏中午放学回家自己煮面条吃.有下面几道工序:①洗锅盛水2分钟;②洗菜3分钟;③准备面条及佐料2分钟;④用锅把水烧开7分钟;⑤用烧开的水煮面条和菜要3分钟.以上各道工序,除④外,一次只能进行一道工序.小敏要将面条煮好,最少用 分钟.
三、解答题:本大题共7小题,共58分.解答题应写出文字说明,推演步骤或证明过程.
18. (本题满分6分) 先化简,再求值: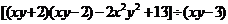 ,其中:
,其中: 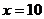 ,
,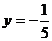 .
.
19. (本题满分8分)从某市中学参加初中毕业考试的学生成绩中抽取40名学生的数学成绩,分数如下:90,86,61,86,73,86,91,68,75,65,72,81,86,99,79,80,86,74,83,77,86,93,96,88,87,86,92,77,98,94,100,86,64,100,69,90,95,97,84,94.这个样本数据的频率分布表如下表:
分 组
频数累计
频数
频率
59.5-64.5
?
2
0.050
64.5-69.5
?
3
0.075
69.5-74.5
?
3
0.075
74.5-79.5
?
4
0.100
79.5-84.5
?
4
84.5-89.5
正正
10
0.250
89.5-94.5
正?
7
0.175
94.5-99.5
正
5
0.125
99.5-104.5
?
2
0.050
(1)这个样本数据的众数是多少?
(2)在这个表中,数据在79.5-84.5的频率是多少?
(3)估计该校初中毕业考试的数学成绩在85分以上的约占百分之几?
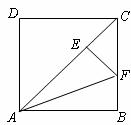
20. (本题满分8分) 如图,在正方形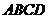 的对角线
的对角线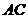 上取一点
上取一点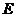 ,使
,使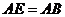 ,过
,过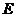 作
作 交
交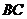 于
于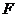 .
.
(1)求证: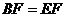 ; (2)求
; (2)求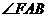 的度数.
的度数.
21. (本题满分8分) 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需甲种原料9kg、乙种原料3kg;生产一件B种产品需甲种原料4kg、乙种原料10kg.
(1)设生产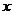 件A种产品,写出
件A种产品,写出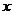 应满足的不等式组;
应满足的不等式组;
(2)有哪几件符合题意的生产方案?请你帮助设计.
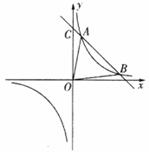
22. (本题满分8分) 如图,已知一次函数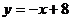 和反比例函数
和反比例函数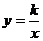 图象在第一象限内有两个不同的公共点
图象在第一象限内有两个不同的公共点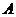 、
、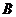 .
.
(1)求实数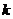 的取值范围;
的取值范围;
(2)若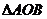 的面积
的面积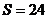 ,求
,求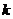 的值.
的值.
23. (本题满分10分) 某产品每件的成本是120元,为了解市场规律,试销阶段按两种方法进行销售,结果如下:
方案甲:保持每件150元的售价不变,此时日销售量为50件;
方案乙:不断地调整售价,此时发现日销售量y(件)是售价x(元)的一次函数,且前三天的销售情况如下表:
x(元)
130
150
160
y(件)
70
50
40
(1)如果方案乙中的第四天、第五天售价均为180元,那么前五天中,哪种方案的销售总利润大?
(2)分析两种方案,为获得最大日销售利润,每件产品的售价应写为多少元?此时,最大日销售利润S是多少?
(注:销售利润=销售额-成本额,销售额=售价×销售量)
24. (本题满分10分) 如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时,水池DEFG的面积最大?
⑶实际施工时,发现在AB上距B点1.85的M处有一棵大树,判断这棵大树是否位于最大矩形水池的边上.