2007-2008学年(上)东北师大附中九年级第二次月考
数 学 试 卷
(满分120分 时间120分钟)
一、选择题(每小题3分,共24分)
1.方程(x-2)(x-1)=0的解是 ( )
A.x1=1,x2=0 B.x1=1,x2=2
C.x1=2,x2=-1 D.无解
2.抛物线y=3(x-4)2+5的顶点坐标为 ( )
A.(4,5) B.(-5,5) C.(4,-5) D.(-4,-5)
3.已知在Rt△ABC中,∠C=90°,AC=12,AB=13,那么tanB的值是 ( )
A.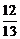 B.
B.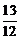 C.
C.
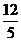 D.
D.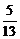
4.在Rt△ABC中,∠C=90°,斜边AB=15,sinA=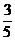 ,则∠A的对边的长为 ( )
,则∠A的对边的长为 ( )
A.25 B.
5.已知⊙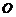 的圆心在坐标原点上,半径为
的圆心在坐标原点上,半径为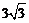 ,点
,点 的坐标是(4,3),则
的坐标是(4,3),则 点与⊙
点与⊙ 的位置关系是 ( )
的位置关系是 ( )
A.在⊙O上 B.在⊙O外
C.在⊙O内 D.在⊙O上或⊙O内
6.如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是 ( )
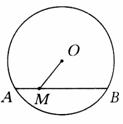
A.3≤OM≤5 B.4≤OM≤5
C.3<OM<5 D.4<OM<5
7.若y=(m-5)x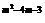 为y关于x的二次函数,则m的值为 ( )
为y关于x的二次函数,则m的值为 ( )
A.m=5 B.m=-
8.下列判断中唯一正确的是 ( )
A.函数y=ax2的图象开口向上,函数y=-ax2的图象开口向下
B.二次函数y=ax2,当x<0时,y随x的增大而增大
C.y=2x2与y=-2x2图象的顶点、对称轴、开口方向、开口大小完全相同
D.抛物线y=ax2与y= -ax2的图象关于x轴对称
二、填空题(每小题3分,共18分)
9.方程ax2-2=0的一个根为1,则a的值为 ;
10.已知在y=-2x2-1与y=-4x2+2的图象组成的图形上,函数的最大值为 .
11.在Rt△ABC中,∠C=90°,∠B=30°,BC=2,则AB= .
12.矩形的四个顶点在同一个圆周上,此圆的圆心位置是 .
13.抛物线y=ax2+a的顶点在y=-2下方,则此抛物线的开口方向是向 .
14.抛物线y=3(x+3)2+2的对称轴是 .
三、计算题(每小题5分,共20分)
15.解方程: 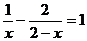
16.计算: sin046°+sin30°-tan260°
17.已知在楼AC顶观测地面目标B的俯角为30°,楼AC高

18.在⊙O中,AB为⊙O的弦,半径OA=6,∠A=30°,求弦AB的长.

四、解答题(每小题6分,共12分)
19.已知:x=1是方程x2+tanAx-2=0的一个解,求锐角∠A的度数.
20.一条抛物线以y轴为对称轴,顶点在原点,且过点(3,2),求这条抛物线的解析式.
五、解答题(每小题6分,共12分)
21.长为

22.如图AB是⊙O的直径,弦 CD⊥AB于E,BE=4,CD=16,求⊙O的半径.

六、解答题(每小题7分,共14分)
23. 市政府为了解决老百姓看病贵的问题,决定下调一些药品的价格.某种药品原售价为125元/盒,连续两次降价后售价为80元/盒,假设每次降价的百分率相同,求这种药品每次降价的百分率.
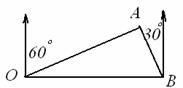
24.游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求灯塔A到航线OB的最短距离(答案含根号).
七、解答题(每小题10分,共20分)
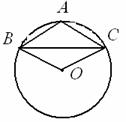
25.已知BC为⊙O的弦,将△OBC沿BC翻转,则点O落在⊙O的圆周A点,OB=5,.
(1)求BC 的长;
(2)将△ABC绕点B顺时针旋转120°,点A到点D的位置,求AD的长.
26.如图,已知开口向上的抛物线经过原点,与x轴的另一个交点为A,OA=6,P为抛物线的顶点,且∠APO=90°.
(1)求这个抛物线的解析式;
(2)若将这个抛物线的顶点向上平移到x轴上,则新的抛物线的解析式为 ;
(3)新的抛物线与y轴交于点B,求△BOP的面积S△BOP.