2006-2007学年度烟台市招远第二学期第一学段考试
初二数学试题
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分.
整个试卷满分为120分.
一、选择题:(将唯一正确答案代号填在括号内.每小题2分。满分30分)
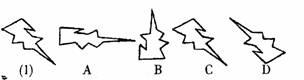
1.如图是五幅“闪电形”图案,通过平移图案(1)可以得到图案 ( )
2.平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是 ( )
A.1:2:3:4 B.3:4:4:3 C.3:3:4:4 D.3:4:3:4
3.下列图形绕某点旋转后,不能与原来重合的是(旋转度数不超过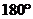 ) ( )
) ( )
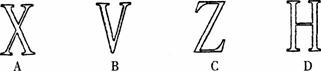
4.能把矩形分成周长相等的两部分的直线有 ( )
A.1条 B.2条 C.4条 D.无数条
5.菱形的两条对角线长分别是6cm和8cm,则菱形的边长是 ( )
A.5cm B.7cm C.8cm D.10cm
6.下列图形变换中,不是旋转变换的是 ( )

7.下列美丽的图案中,既是轴对称图形又是中心对称图形的个数是 ( )

A.1个 B.2个 C.3个 D.4个
8.如图,在直角坐标系中,网格线是由若干个边长为1的小正方形拼成的.△ABC与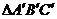 的顶点都是小正方形的顶点.若将△ABC平移后得到
的顶点都是小正方形的顶点.若将△ABC平移后得到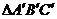 ,则正确的平移方法是
( )
,则正确的平移方法是
( )
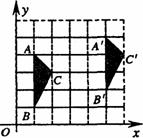
A.先向下平移l格,再向右平移4格
B.先向上平移l格,再向右平移4格
C.先向上平移l格,再向右平移3格
D.先向下平移l格,再向右平移3格
9.如图,EF经过平行四边形ABCD对角线的交点O,AB=4,AD=3,OF=1.3,则平行四边形ABCD的周长与四边形BCEF的周长之差为 ( )
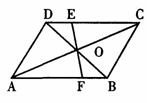
A.4.4 B.5.4 C.8.4 D.9.4
10.在学习四边形时,小明的书上有一图因不小心被滴上墨水(如图),看不清所印的字,请问被墨水遮盖的文字应是 ( )

A.等边三角形 B.四边形 C.等腰梯形 D.菱形
11.多边形的每个内角都等于l50°,则从此多边形的一个顶点出发可作的对角线共有 ( )
A.8条 B.9条 C.10条 D.11条
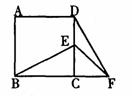
12.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转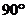 得到△DCF,连结EF,若
得到△DCF,连结EF,若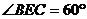 ,则∠EFD的度数为 ( )
,则∠EFD的度数为 ( )
A.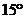 B.
B.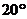 C.
C. D.
D.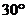
13.如图,在等腰梯形ABCD中,AD∥BC,AC与BD交于点O,∠ADB=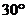 ,∠DCB=
,∠DCB=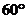 ,则图中的等腰三角形共有 ( )
,则图中的等腰三角形共有 ( )
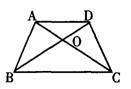
A.4个 B.3个 C.2个 D.1个
14.已知正方形ABCD的边长为2,E、F分别是BC和CD边上的中点,则△AEF的面积为 ( )
A.2
B.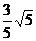 C.
C.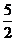 D.
D.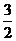
15.下面的基本图案中,经过平移、旋转或轴对称变换后,不能得到图l的是 ( )
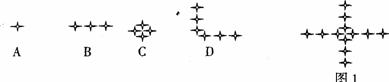
二、填空题:(将正确答案填在横线上.每小题3分。满分30分)
16.一个正方形绕它的中心至少旋转__________度能与自身重合.
17.要说明一个四边形是菱形,可以先说明这个四边形是___________,再说明______(只需填写一种方法即可).
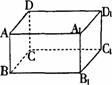
18.在如图所示的长方体中,可以由线段AB平移而得到的线段有__________条.
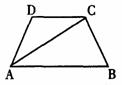
19.如图,在梯形ABCD中,DC∥AB,AD=BC,AC平分∠DAB,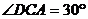 ,DC=3厘米,则梯形ABCD的周长为___________.
,DC=3厘米,则梯形ABCD的周长为___________.
20.一个多边形的内角和是外角和的3倍,则这个多边形是_____________边形.
21.将一条2厘米的斜线向右平移3厘米,连结对应点得到四边形的周长为___________.
22.如图的图案是由正方形、正三角形和________密铺而成的.
23.风扇在旋转过程中,旋转一周的周长为95cm,若风扇旋转了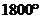 ,则旋转的总长度为_________cm.
,则旋转的总长度为_________cm.
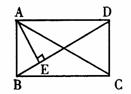
24.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为_____.
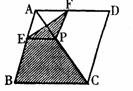
25.如图,菱形ABCD的对角线的长分别为4和5,P是对角线AC上任一点,且PE∥BC交AB于E,PF∥CD交AD于F.则图中阴影部分的面积是_______________.
三、解答题:(每小题6分.满分l2分)
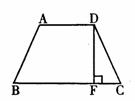
26.如图,在等腰梯形ABCD中,AD=2,BC=4,高DF=2.求腰DC的长.
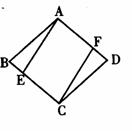
27.如图,点E、F分别在菱形ABCD的边BC、AD上,且AF=CE,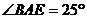 ,
,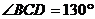 ,求∠AFC的度数.
,求∠AFC的度数.
四、画图题:(每小题7分,满分l4分)
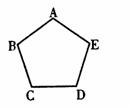
28.将五边形ABCDE(如图)沿水平方向向右平移3.5cm(要求:画出图形,写出解答)
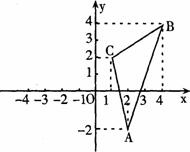
29.如图,△ABC的顶点坐标分别为A(2,-2),B(4,4),C(1,2).将△ABC绕坐标原点O逆时针旋转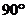 ,得到
,得到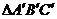 (
(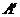 、
、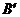 、
、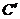 分别为A、B、C的对应点),在坐标系中画出
分别为A、B、C的对应点),在坐标系中画出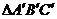 ,并写出
,并写出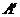 、
、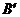 、
、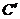 三点的坐标.
三点的坐标.
五、探索题:(每小题9分,满分l8分)
30.如图,在梯形ABCD中,AD∥BC,∠B=∠C,E是BC边的中点.请你探索线段AE与DE间的数量关系,并说明理由.
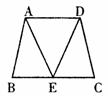
31.如图,点C在线段AB上,△ADC和△CEB都是等边三角形,连结AE交DC于N,连结BD交EC于M.则△MCB可看作是由△NCE经过旋转而得到的.请回答下列问题:
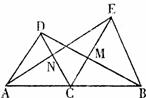
(1)旋转中心点是___________;
(2)旋转角的度数是_______________;
(3)连结MN,则△MNC是什么三角形__________________;
(4)△DCB和△ACE是否全等,为什么?
六、操作与解释题:(满分11分)
32.如图,某村有一个四边形的池塘,在它的四个角A、B、C、D处各有一棵古树,现村民要在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍
(1)问:这种设想能否实现?若能实现,请你设计一下;若不能,请说明理由.
(2)你设计的方案是什么图形,请说明理由.