2006年江苏省苏州工业园区初三调研试卷
第Ⅰ卷(选择题,共27分)
一、选择题:本大题共9小题;每小题3分,共27分,在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知点P(2,-1)与点Q关于x轴对称,则点Q的坐标为
A.(-2,1) B. (-2,-1) C. (2,1) D. (2,-1)
 2.如图,在等腰直角Rt△ABC中,
2.如图,在等腰直角Rt△ABC中,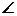 B=
B=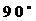 ,将△ABC绕着顶点A沿
,将△ABC绕着顶点A沿
逆时针方向旋转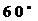 后得到△
后得到△ ,则
,则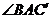 等于
等于
A. 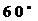 B.
B. 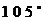 C.
C. 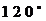 D.
D. 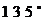
3.下列四个函数中,y随x增大而减小的是
A.y=3x B. y=?3x+ D. .y=?x2+3x?1
D. .y=?x2+3x?1
4.将方程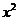 +4x+1=0配方后,原方程变形为
+4x+1=0配方后,原方程变形为
A.
(x+2)2=3 B. (x+4)2=
5.下列交通指示牌图形中,轴对称图形的个数是
A.1个 B.2个 C.3个 D.4个.
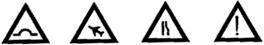
6.如图,CD是 斜边AB上的高,将
斜边AB上的高,将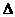 BCD沿CD折叠,B
BCD沿CD折叠,B
点恰好落在AB的中点E处,则 A等于
A等于
A.25 B.
B.  C. 45
C. 45 D. 60
D. 60
7.一架长2.5 米的梯子,斜立在一竖直的墙上,这时梯足距墙底端
0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将滑
A.0.8米 B. 1.5米 C. 0.9米 D. 0.5米
 8.小明把自己一周的支出情况,用如图所示的统计图来表示,下面说法正确的是
8.小明把自己一周的支出情况,用如图所示的统计图来表示,下面说法正确的是
A.从图中可以直接看出具体消费数额
B.从图中可以直接看出总消费数额
C.从图中可以直接看出各项消费数额占总消费额的百分比
D.从图中可以直接看出各项消费数额在一周中的具体变化情况
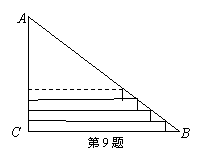 9.红星中学高二(2)班在布置“五.四”青年节联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条。如图所示:在Rt△ACB中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数
9.红星中学高二(2)班在布置“五.四”青年节联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条。如图所示:在Rt△ACB中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数
A. 24 B. 25 C. 26 D. 27
. 第Ⅱ卷(非选择题,98分)
得分
评卷人
复评人
二、填空题:本大题共8小题,每小题3分,共24分,把答案填在题中横线上
10.-2的倒数是 .
 11.苏州工业园区正建设成为具有国际竞争力的高科技工业园区和现代化、园林化、国际化的新城区.2005年,全区实现地区生产总值达580.7亿元,比开发之初增长了50倍。请你用科学计数法表示2005年园区生产总值为 元
11.苏州工业园区正建设成为具有国际竞争力的高科技工业园区和现代化、园林化、国际化的新城区.2005年,全区实现地区生产总值达580.7亿元,比开发之初增长了50倍。请你用科学计数法表示2005年园区生产总值为 元
12.右图是某物体的三视图,那么该物体形状是 .
13.因式分解:2x2-8= .
 14.某班有7名同学参加校“综合素质智能竞赛”,成绩(单位:分)分别是87,92,87,89,91,88,76.则它们成绩的众数是 分,中位数 分.
14.某班有7名同学参加校“综合素质智能竞赛”,成绩(单位:分)分别是87,92,87,89,91,88,76.则它们成绩的众数是 分,中位数 分.
15.如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最大视角∠COD= 度,(不考虑青蛙的身高);

16.如图,测量小玻璃管口径的量具ABC,AB的长为12cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是 cm。
 17.如图两个相同的梯形重叠在一起,则上面的梯形中未重叠部分面
17.如图两个相同的梯形重叠在一起,则上面的梯形中未重叠部分面
积是
(第18~20题,每题5分,共15分)
三、解答题:本大题共12小题,共74分,解答应写出必要的计算过程、推演步骤或文字说明
18.计算: 22+(4-7)÷+()
19.先化简,再求值: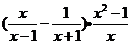 ,其中
,其中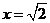
20.解不等式组: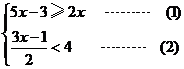
(第21~22题,每题6分,共12分)
21、旋转是一种常见的全等变换,图⑴中 绕点
绕点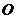 旋转后得到
旋转后得到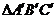 ,我们称点
,我们称点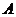 和点
和点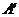 、点
、点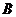 和点
和点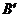 、点
、点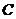 和点
和点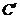 分别是对应点,把点
分别是对应点,把点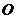 称为旋转中心。
称为旋转中心。
⑴观察图1,想一想,旋转变换具有哪些特点呢?请写出其中二个特点:
___________________________________________________________________
___________________________________________________________________
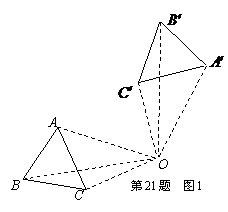
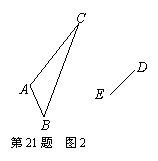
⑵图2中, 顺时针旋转后,线段
顺时针旋转后,线段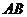 的对应线段为线段
的对应线段为线段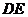 ,请你利用圆规、直尺等工具,①作出旋转中心
,请你利用圆规、直尺等工具,①作出旋转中心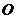 ,②作出
,②作出 绕点
绕点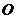 旋转后的
旋转后的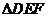 。(不写画法,保留作图痕迹)
。(不写画法,保留作图痕迹)
22.杨文与王小勇两同学玩“奇、偶手指”的游戏,两人约定:每人出右手的若干指头,至少出一根。若两人皆出奇数根指头或两人皆出偶数根指头,则杨文赢;若两人中一人出奇数根指头 ,另外一人出偶数根指头,则王小勇赢。试用树状图求杨文与王小勇谁赢的概率大。(注:杨文出一根指头可简单表示为:文1;王小勇出2根指头可简单表示为:勇2;其余依此类推)
(第23~24题,每题6分,共12分)
 23.如图,⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在弧CB上取一点D,分别作直线CD,ED交直线AB于F,M,连结OC,MC.
23.如图,⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在弧CB上取一点D,分别作直线CD,ED交直线AB于F,M,连结OC,MC.
(1) 求∠AOC和∠MDF的度数;
(2) 求证:△MDF∽△MOC.
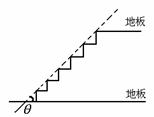
24, 在建筑楼梯时,设计者要考虑楼梯的安全程度,如图1,虚线为楼梯的斜度线,斜度线与地板的
夹角为倾角θ,一般情况下,倾角θ愈小,楼梯的安全程度愈高.
如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角由θ1 减至θ2 ,这样楼梯占用地板的
长度由d1增加到d2,已知d1=4m,∠ACB=∠θ1 =400,∠ADB=∠θ2 =360,求楼梯占用地板的长度增加
了多少? (精确到0.01m)
 |
|||
 |
|||
第24题 图1 第24题 图2
(第25~26题,每题6分,共12分)
 有这样一道题目:“已知:二次函数
有这样一道题目:“已知:二次函数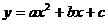 的图像经过点A(0,a),B(l,-2),与x轴的一个交点 ,求证:这个二次函数图像的对称轴是直线x=2.”
的图像经过点A(0,a),B(l,-2),与x轴的一个交点 ,求证:这个二次函数图像的对称轴是直线x=2.”
题目中的矩形框部分是一段被墨水染污了无法辨认的文字.
(1)根据现有的信息,你能否求出题目中二次函数的解析式?若能,写出求解过程;若不能,说明理由.
(2)请你根据已有信息,把原题补充完整。
26、为测算园区市民用水量,小明同学到园区某小区进行用水统计,下表是该小区五月份部分用户的用水情况:
月用水量(米3)
4
5
6
8
9
11
户数
2
3
7
5
2
1
 (1)计算20户家庭的月平均用水量;
(1)计算20户家庭的月平均用水量;
(2)画出这20户家庭月用水量的频数分布直方图;
(3)如果该小区有500户家庭,根据上面的计算结果,
估计该小区居民每月共用水多少立方米?
27.(本题7分)
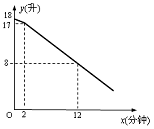 教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接
教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接
水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?(3)按(2)的放水方法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?
28、(本题8分)
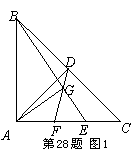
已知:如图1,在Rt△ABC中,∠BAC= 90°,AB= AC,D为BC的中点,E为AC上一点,点G在BE上,连结DG并延长交AE于F,若∠FGE= 45°,
(1)求证:BD?BC= BG?BE;
(2)求证:AG⊥BE;
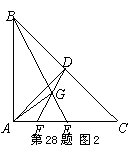
(3)如图2,若E为AC的中点,求EF∶FD的值。
29.(本题8分)
如图1,已知抛物线的顶点为A(O,1),矩形CDEF的顶点C、F在抛物线上,D、E在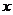 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.
(1)求此抛物线的解析式;
(2)如图2,若P点为抛物线上不同于A的一点,连结PB并延长交抛物线于点Q,过点P、Q分别作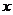 轴的垂线,垂足分别为S、R.
轴的垂线,垂足分别为S、R.
①求证:PB=PS;
②判断△SBR的形状;
③试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似,若存在,求出M点坐标;若不存在,请说明理由.