2006-2007学年度江苏省盐城市盐城中学初三年级
第一学期期中试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1、已知方程x2-x+1=0,则……………………………………………………… ( )
A、方程有两个不相等的实数根 B、方程有两个相等的实数根
C、方程没有实数根 D、方程只有一个实数根
2、已经有两个正方形瓷砖,再用几个边长相等的正三角形瓷砖就可以在一个点周围进行平面镶嵌 …………………………………………………………………………… ( )
A、2个 B、3个 C、4个 D、5个
3、下列语句中,正确的是………………………………………………………… ( )
A、同一平面上三点确定一个圆;
B、三角形的外心是三角形三边中垂线的交点;
C、三角形的外心到三角形三边的距离相等;
D、菱形的四个顶点在同一个圆上.
4、方程x(x-2)=x-2的根为 ………………………………………………………( )
A、x1=1,x2=2 B、x1=0,x2=
5、如图,点A、B、C在⊙O上,AO∥BC,∠OAC=20°,则∠AOB的度数是( )
A、10° B、20° C、40° D、70°
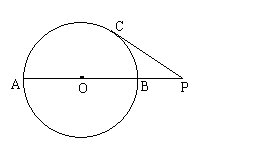
6、如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2则PC等于…………………………………………………………………………………( )
A、2
B、
7、如图,若点O是△ABC的内心,∠ABC=80°,∠ACB=60°则∠BOC的度数为( )
 A、140°
B、130°
C、120°
D、110°
A、140°
B、130°
C、120°
D、110°
| ||||||||||||||||||||||||||||||||||||||||||
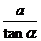
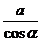 9、如图所示,B为建筑物的最高点,从地面上的点A用测角仪测得B点的仰角(即
9、如图所示,B为建筑物的最高点,从地面上的点A用测角仪测得B点的仰角(即
 A、
A、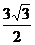 B、
B、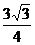 C、
C、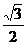 D、
D、
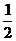 ,则锐角α= °.
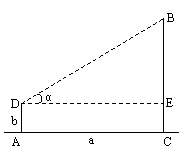
,则锐角α= °.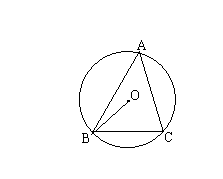 14、为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在水平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=
14、为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在水平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=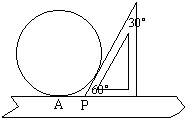
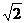 sin60°cos45°+
sin60°cos45°+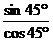
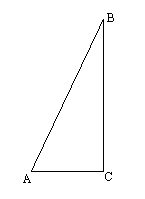

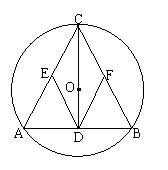 23、(本小题共7分)已知:如图,⊙O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点.判断四边形CEDF的形状并说明理由.
23、(本小题共7分)已知:如图,⊙O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点.判断四边形CEDF的形状并说明理由.

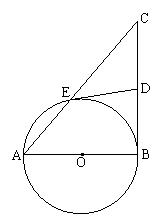 25、(本小题共8分)如图所示,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点E,点D是BC边的中点,连接ED.
25、(本小题共8分)如图所示,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点E,点D是BC边的中点,连接ED.
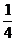 圆时所做成的圆锥的锥角(锥角:即圆锥经过轴的截面上两条母线的夹角,例如图1中∠AOB);
圆时所做成的圆锥的锥角(锥角:即圆锥经过轴的截面上两条母线的夹角,例如图1中∠AOB);


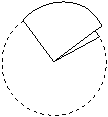

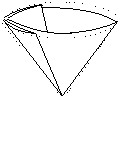
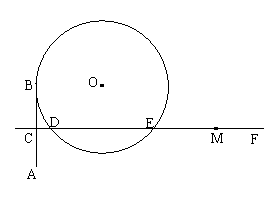
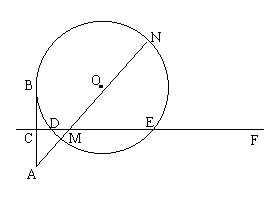 (3)当点M在射线EF上时,若a为小于17的正数,问是否存在这样的a,使得直线AM与⊙O相切?若存在,求出a的值;若不存在,试说明理由.
(3)当点M在射线EF上时,若a为小于17的正数,问是否存在这样的a,使得直线AM与⊙O相切?若存在,求出a的值;若不存在,试说明理由.