摘要:已知:AB切⊙O于点B.线段AB的垂直平分线CF交AB于点C.交⊙O于点D.E.设点M是射线CF上的任一点.CM=a.连接AM.若CB=3.DE=8.(1)求⊙O 半径及线段CD的长,(2)当M在线段DE上时.延长AM交⊙O于点N.连接NE.若△ACM∽△NEM.求NE,
网址:http://m.1010jiajiao.com/timu_id_658538[举报]
(本小题满分10分)已知,等腰Rt△ABC中,点O是斜边的中点,△MPN是直角三角形,固定△ABC,滑动△MPN,在滑动过程中始终保持点P在AC上,且 PM⊥AB,PN⊥BC,垂足分别为E、F.

(1)如图1,当点P与点O重合时,OE、OF的数量和位置关系分别是____ __.
(2)当△MPN移动到图2的位置时,(1)中的结论还成立吗?请说明理由.
(3)如图3,等腰Rt△ABC的腰长为6,点P在AC的延长线上时,Rt△MPN的边PM
与AB的延长线交于点E,直线BC与直线NP交于点F,OE交BC于点H,且 EH: HO=2:5,则BE的长是多少?
查看习题详情和答案>>
(本小题满分10分)
已知直线y= 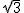 x+4
x+4
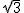 与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
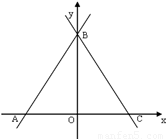
1.(1)试确定直线BC的解析式.
2.(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与 t 的函数关系式,并写出自变量的取值范围.
3.(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
查看习题详情和答案>>
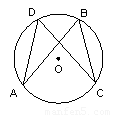
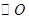 的两条弦, 且
的两条弦, 且 .求证:
.求证: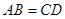 .
. 
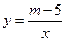 (
( 为常数)图象的一支.
为常数)图象的一支.
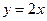 的图象在第一象内限的交点为
的图象在第一象内限的交点为 ,过
,过 轴的垂线,垂足为
轴的垂线,垂足为 ,当
,当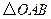 的面积为4时,求点
的面积为4时,求点